Angulos Internos E Externos De Poligonos Exe 1 2 3 Geogebra
ángulos Internos Y Externos De Polígonos Regulares Geogebra Ângulos internos e externos de polígonos (exe 1,2,3) autor: sandra bolinhas. topico (s): Ângulos, polígonos. tarefa: Ângulos internos e externos de polígono (exe 1, 2 e 3) depois de resolveres os exercícios, envia as tuas respostas para a disciplina no moodle. Geogebra classroom. esboço. Ângulos internos e externos de um polígono. Ângulos internos e externos de polígonos (exe 1,2,3) Ângulos internos e externos de polígonos (exe 4) tarefa: Ângulos internos e externos de polígonos (exe 5) Ângulos internos e externos de um polígono. autor:sandra bolinhas. topico(s):Ângulos.

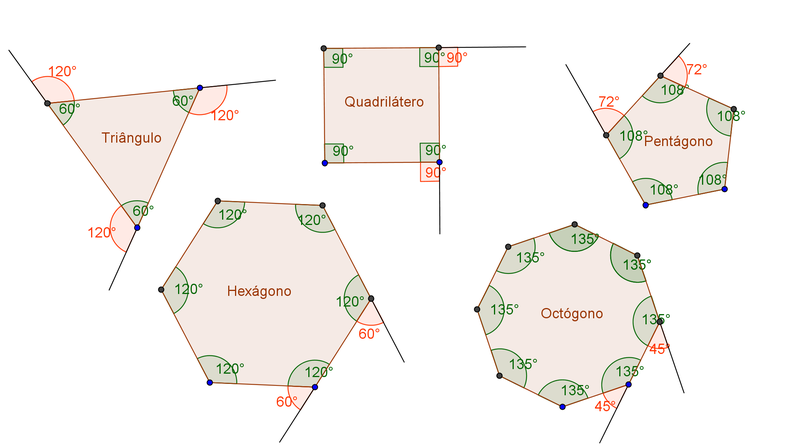
ângulos Internos E Externos De Polígonos Exe 1 2 3 Geogebra Polígonos – geogebra. calculadoras. estudando formas, tamanhos e relações espaciais em matemática. mapeamento de relações de entradas para saídas específicas em matemática. investigar sequências e séries, resolver equações diferenciais. estudando ângulos, triângulos, funções e razões trigonométricas. Ângulos internos e externos de um polígono. os ângulos internos de um polígono regular podem ser calculados usando uma fórmula. essa fórmula nos permite calcular sua soma com base no número de lados do polígono. por outro lado, a soma dos ângulos externos de qualquer polígono é sempre igual a 360°. assim, a medida de cada ângulo é. Polígonos. polígonos são figuras planas e fechadas, ou seja, limitadas por segmentos de retas. os polígonos têm como elementos: lados, vértices, ângulos e diagonais. representação de um. Para calcular a soma dos ângulos internos de um polígono, utiliza se a fórmula s= (n−2)×180°, onde s é a soma dos ângulos internos e n é o número de lados do polígono. para os ângulos externos, independentemente do número de lados do polígono, a soma dos ângulos externos é sempre 360°, considerando que cada ângulo externo é.

ângulo Interno E Externo De Um Polígono Soma Dos ângulos Internos De Polígonos. polígonos são figuras planas e fechadas, ou seja, limitadas por segmentos de retas. os polígonos têm como elementos: lados, vértices, ângulos e diagonais. representação de um. Para calcular a soma dos ângulos internos de um polígono, utiliza se a fórmula s= (n−2)×180°, onde s é a soma dos ângulos internos e n é o número de lados do polígono. para os ângulos externos, independentemente do número de lados do polígono, a soma dos ângulos externos é sempre 360°, considerando que cada ângulo externo é. Calculemos a soma dos ângulos internos de um polígono com quatro lados. a figura nos mostra que um ângulo desconhecido é três vezes maior que o outro. somando os quatro valores: assim, o menor ângulo é de 45º, os intermediários são iguais a 90º e o maior, três vezes 45º, possui 135º. logo, a resposta correta é a letra d) 45º. Por su parte, la suma de los ángulos internos de cualquier polígono es calculada usando la siguiente fórmula: (n − 2) × 1 8 0. (n 2)\times 180 (n− 2) × 180 °. en donde, n es el número de lados del polígono. por ejemplo, en el caso de un hexágono, usamos n=6 n = 6. podemos usar esta fórmula para calcular la suma de ángulos.

Comments are closed.