Angulos Externos De Poligonos Formula E Exemplos Neurochispas
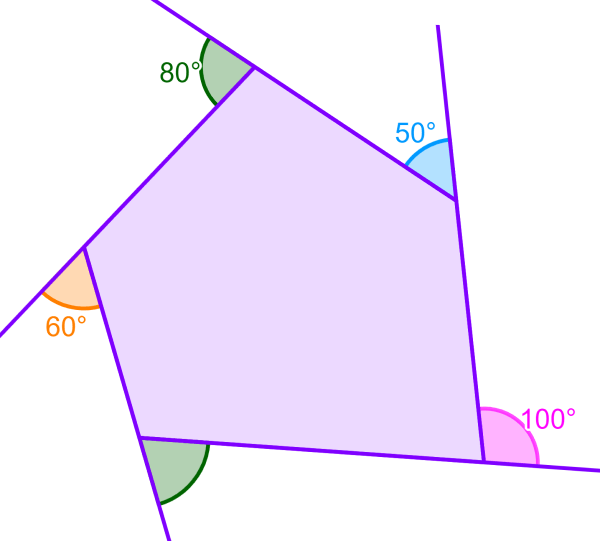
ângulos Externos De Polígonos Fórmula E Exemplos Neurochispas Por exemplo, se temos os ângulos externos 60°, 70°, 80° e 85° em um pentágono, temos que começar determinando sua soma e depois subtrair de 360°: 60° 70° 80° 85°=295°. ⇒ 360° 295°=65°. a medida do ângulo que falta é 65°. além disso, também podemos calcular as medidas dos ângulos externos se conhecermos as medidas dos. Por ejemplo, si es que tenemos los ángulos interiores 90°, 120°, 110°, 105° y 115° en un pentágono, tenemos que restar cada ángulo de 180° para encontrar los ángulos exteriores correspondientes: 180° 90°=90°. 180° 120°=60°. 180° 110°=70°. 180° 105°=75°. 180° 115°=65°.
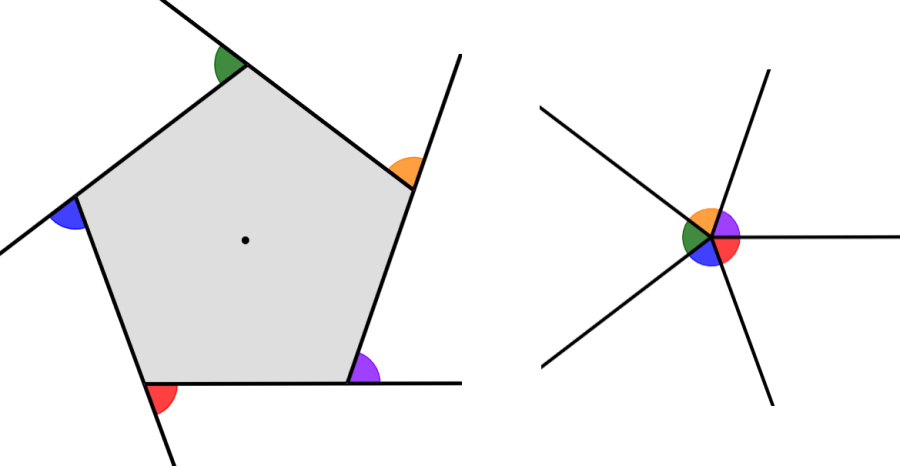
ângulos Externos De Polígonos Fórmula E Exemplos Neurochispas Podemos ver que todos os ângulos externos de um polígono têm uma soma total de 360°. portanto, podemos encontrar a medida de um dos ângulos externos de um polígono regular dividindo 360° pelo número de lados do polígono regular. por exemplo, para um pentágono, temos: 360°÷5=72°. cada ângulo externo de um pentágono regular mede 72°. A soma dos ângulos externos de um triângulo é sempre igual a 360°. assim, dependendo do tipo de triângulo, podemos aplicar diferentes métodos para encontrar a medida de cada ângulo. a seguir, aprenderemos como determinar a medida dos ângulos externos de diferentes tipos de triângulos. além disso, veremos alguns exemplos de prática. 180° 70°=110°. la medida del ángulo a es 110°. ahora, restamos este ángulo de 360° para encontrar las medidas de los otros dos ángulos externos: 360° 110°=250°. esto corresponde a la suma de ambos ángulos. dado que ambos ángulos son iguales, dividimos la suma por 2 y tenemos: 250°÷2=125°. los ángulos b y c miden 125°. Por su parte, la suma de los ángulos internos de cualquier polígono es calculada usando la siguiente fórmula: (n − 2) × 1 8 0. (n 2)\times 180 (n− 2) × 180 °. en donde, n es el número de lados del polígono. por ejemplo, en el caso de un hexágono, usamos n=6 n = 6. podemos usar esta fórmula para calcular la suma de ángulos.
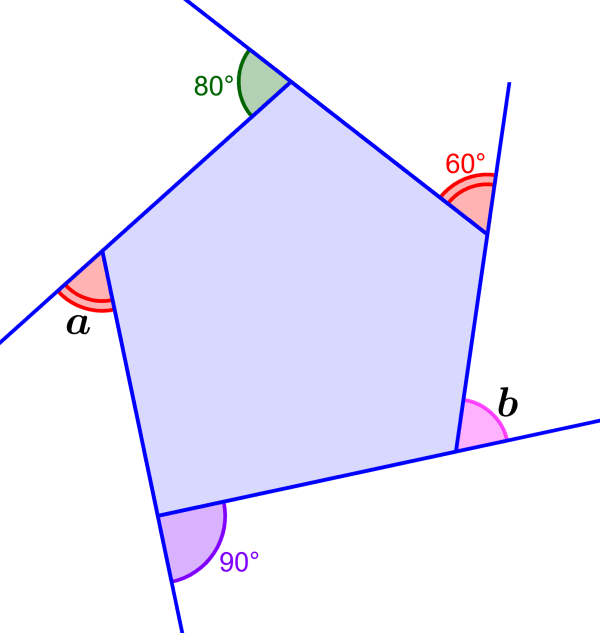
ângulos Externos De Polígonos Fórmula E Exemplos Neurochispas 180° 70°=110°. la medida del ángulo a es 110°. ahora, restamos este ángulo de 360° para encontrar las medidas de los otros dos ángulos externos: 360° 110°=250°. esto corresponde a la suma de ambos ángulos. dado que ambos ángulos son iguales, dividimos la suma por 2 y tenemos: 250°÷2=125°. los ángulos b y c miden 125°. Por su parte, la suma de los ángulos internos de cualquier polígono es calculada usando la siguiente fórmula: (n − 2) × 1 8 0. (n 2)\times 180 (n− 2) × 180 °. en donde, n es el número de lados del polígono. por ejemplo, en el caso de un hexágono, usamos n=6 n = 6. podemos usar esta fórmula para calcular la suma de ángulos. A soma dos ângulos externos de um polígono convexo sempre deve ser igual a 360°. esse resultado não depende da quantidade e da medida de lados e ângulos desse figura. Ângulos externos de um hexágono regular. entre os elementos de um polígono, estão os lados, vértices, ângulos internos e ângulos externos. quando o polígono é. Por exemplo, todo polígono com três lados é classificado como triângulo, enquanto todo com quatro lados, como quadriláteros. conforme a classificação quanto ao número de lados, os polígonos recebem nomes. aqui estão alguns. um polígono por ter muitos lados, e conforme a quantidade, torna se pouco prático ilustrá los.
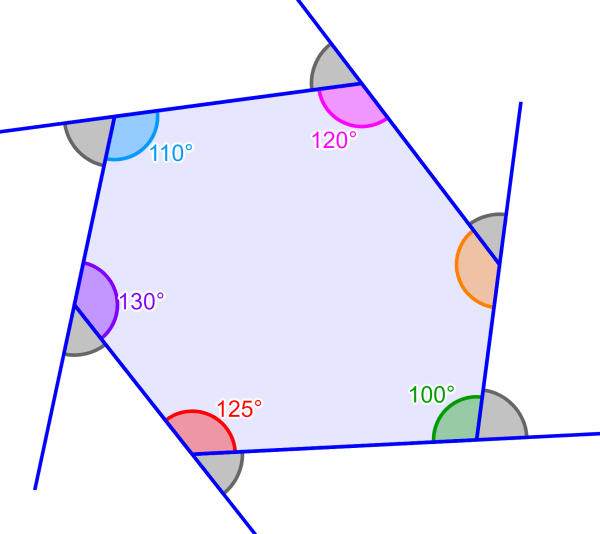
ângulos Externos De Polígonos Fórmula E Exemplos Neurochispas A soma dos ângulos externos de um polígono convexo sempre deve ser igual a 360°. esse resultado não depende da quantidade e da medida de lados e ângulos desse figura. Ângulos externos de um hexágono regular. entre os elementos de um polígono, estão os lados, vértices, ângulos internos e ângulos externos. quando o polígono é. Por exemplo, todo polígono com três lados é classificado como triângulo, enquanto todo com quatro lados, como quadriláteros. conforme a classificação quanto ao número de lados, os polígonos recebem nomes. aqui estão alguns. um polígono por ter muitos lados, e conforme a quantidade, torna se pouco prático ilustrá los.

Comments are closed.