Angle Side Relationships In Triangles Investigation Geogebra
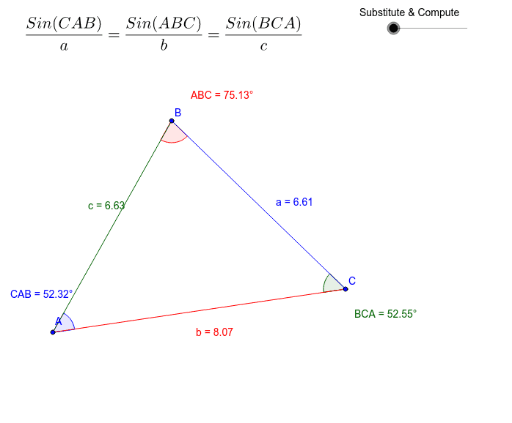
Exploring Side Angle Relationships In Triangles Geogebra Classroom. triangle side angle relationship investigation. author: humberto urgiles, julie morisano. discover the relationship between the sides and angles in one triangle. use the arrow (move) tool to drag the vertices around the page to change the size of the angles and sides. A triangle has the following angle measurements: ma = 170, mb=9, & mc=1. order the sides from least to greatest. a triangle has sides measuring ab = 3, ac = 11, & bc = 9. order the angles of the triangle from least to greatest. a, c, b.
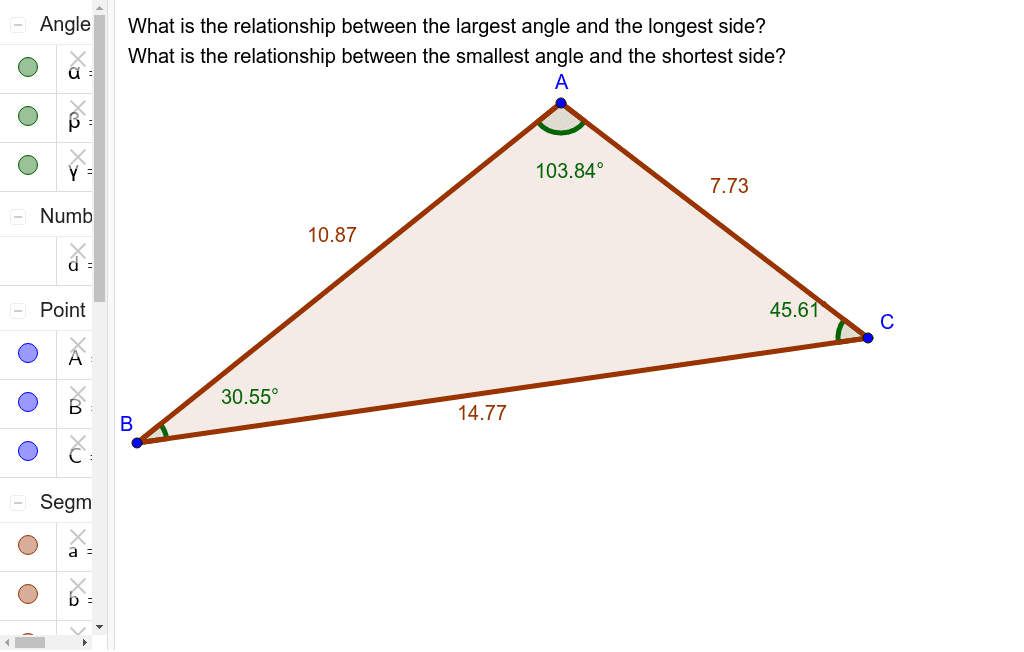
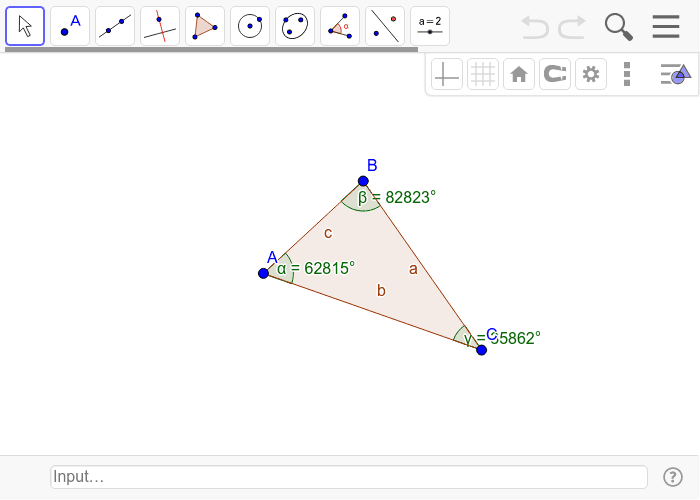
Side Angle Relationships In A Triangle Geogebra Angle side relationships in triangles (investigation) discover resources. equação reduzida da reta; forum 1 154771 a zeigemitlupe. 11) now select the other three lines on your screen. go to display and choose any color that’s different from the color of your triangle interior and the color of the sides of the triangle. 12) now drag the vertices of triangle abc around. as you change the size and shape of this triangle, study how these 3 lines intersect. In such a triangle, the shortest side is always opposite the smallest angle. (these are shown in bold color above) similarly, the longest side is opposite the largest angle. in the figure above, drag any vertex of the triangle and see that whichever side is the shortest, the opposite angle is also the smallest. then click on 'show largest' and. Use the length tool to find the length of segments ab, bb', ac, cc'. do you notice any relationships between these lengths, if so describe them. (hint: compare the ratios of ab and bb' to ac to cc'.) 𝜋. try to moving segment bc to create different triangles, make sure that segments bc and segment b'c' are still parallel.
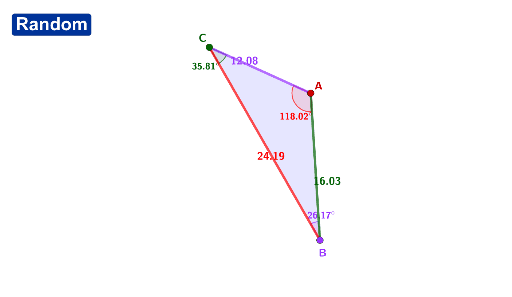
Angle Side Relationships In Triangles Investigation Geogebra In such a triangle, the shortest side is always opposite the smallest angle. (these are shown in bold color above) similarly, the longest side is opposite the largest angle. in the figure above, drag any vertex of the triangle and see that whichever side is the shortest, the opposite angle is also the smallest. then click on 'show largest' and. Use the length tool to find the length of segments ab, bb', ac, cc'. do you notice any relationships between these lengths, if so describe them. (hint: compare the ratios of ab and bb' to ac to cc'.) 𝜋. try to moving segment bc to create different triangles, make sure that segments bc and segment b'c' are still parallel. In a triangle, the angle opposite the longer side is the larger angle. example 1: compare the lengths of the sides of the following triangle. solution: step 1: we need to find the size of the third angle. the sum of all the angles in any triangle is 180º. ∠a ∠b ∠c = 180°. ⇒ ∠a 30° 65° = 180°. ⇒ ∠a = 180° 95°. Explore. day 1: split students into groups of two or three. provide each group with one investigation (either 1a, 1b, or 1c from the "triangle congruence possibilities investigation 1" handout) and a device on which to access geogebra. allow students time to work through their investigations and reach a conclusion.
Angle Side Relationships In A Triangle Geogebra In a triangle, the angle opposite the longer side is the larger angle. example 1: compare the lengths of the sides of the following triangle. solution: step 1: we need to find the size of the third angle. the sum of all the angles in any triangle is 180º. ∠a ∠b ∠c = 180°. ⇒ ∠a 30° 65° = 180°. ⇒ ∠a = 180° 95°. Explore. day 1: split students into groups of two or three. provide each group with one investigation (either 1a, 1b, or 1c from the "triangle congruence possibilities investigation 1" handout) and a device on which to access geogebra. allow students time to work through their investigations and reach a conclusion.

Comments are closed.