An Intuitive Proof Of The Pythagorean Theorem
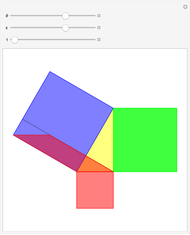
An Intuitive Proof Of The Pythagorean Theorem Wolfram Demonstrations Here is the simplest proof i have seen that doesn't use areas. it just uses similar triangles. however, what is most intuitive is a subjective decision. by similar triangles in the diagram below, we have ca a = a c and cb b = b c. thus, c = ca cb = aa c bb c therefore, c2 = a2 b2. The pythagorean theorem provides an equation to calculate the longer side of a right triangle by summing the squares of the other two sides. it is often phrased as. a2 b2 c2. in this equation, a.
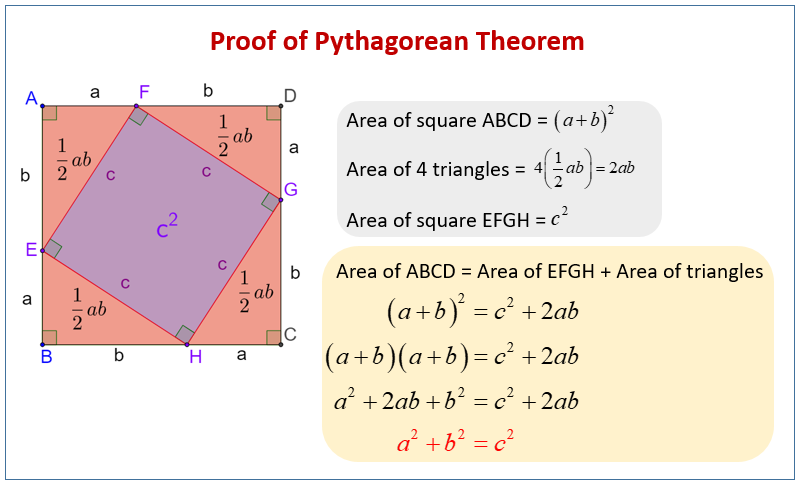
Proving The Pythagorean Theorem Math Liberty When c is a right angle, the blue rectangles vanish and we have the pythagorean theorem via what amounts to proof #5 on cut the knot's pythagorean theorem page. (note that, as mentioned on ctk, the use of cosine here doesn't amount to an invalid "trigonometric proof".) the picture works for obtuse c as well. The mathematical foundation. at its core, the pythagorean theorem is an equation: a 2 b 2 =c 2. where a and b are the lengths of the two legs of a right triangle, and c is the length of the hypotenuse. this relationship holds in all right angled triangles and forms the basis of much of trigonometry, calculus, and even physics. Pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see two squares inside the. The proof of the pythagorean theorem is often the first theorem students learn in geometry, how it is taught can fascinate students or scare them away. an intuitive approach to proving the.

How To Prove The Pythagorean Theorem 10 Steps With Pictures Pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see two squares inside the. The proof of the pythagorean theorem is often the first theorem students learn in geometry, how it is taught can fascinate students or scare them away. an intuitive approach to proving the. Interior angle Δθ = θ 1 −θ 2. the pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that where is the angle between sides and . [45] when is radians or 90°, then , and the formula reduces to the usual pythagorean theorem. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem.

Intuitive Proof Of The Pythagorean Theorem Youtube Interior angle Δθ = θ 1 −θ 2. the pythagorean theorem is a special case of the more general theorem relating the lengths of sides in any triangle, the law of cosines, which states that where is the angle between sides and . [45] when is radians or 90°, then , and the formula reduces to the usual pythagorean theorem. Pythagorean theorem. download wolfram notebook. for a right triangle with legs and and hypotenuse , (1) many different proofs exist for this most fundamental of all geometric theorems. the theorem can also be generalized from a plane triangle to a trirectangular tetrahedron, in which case it is known as de gua's theorem.

Comments are closed.