Alternate Interior Angles Definition Theorem And Examples
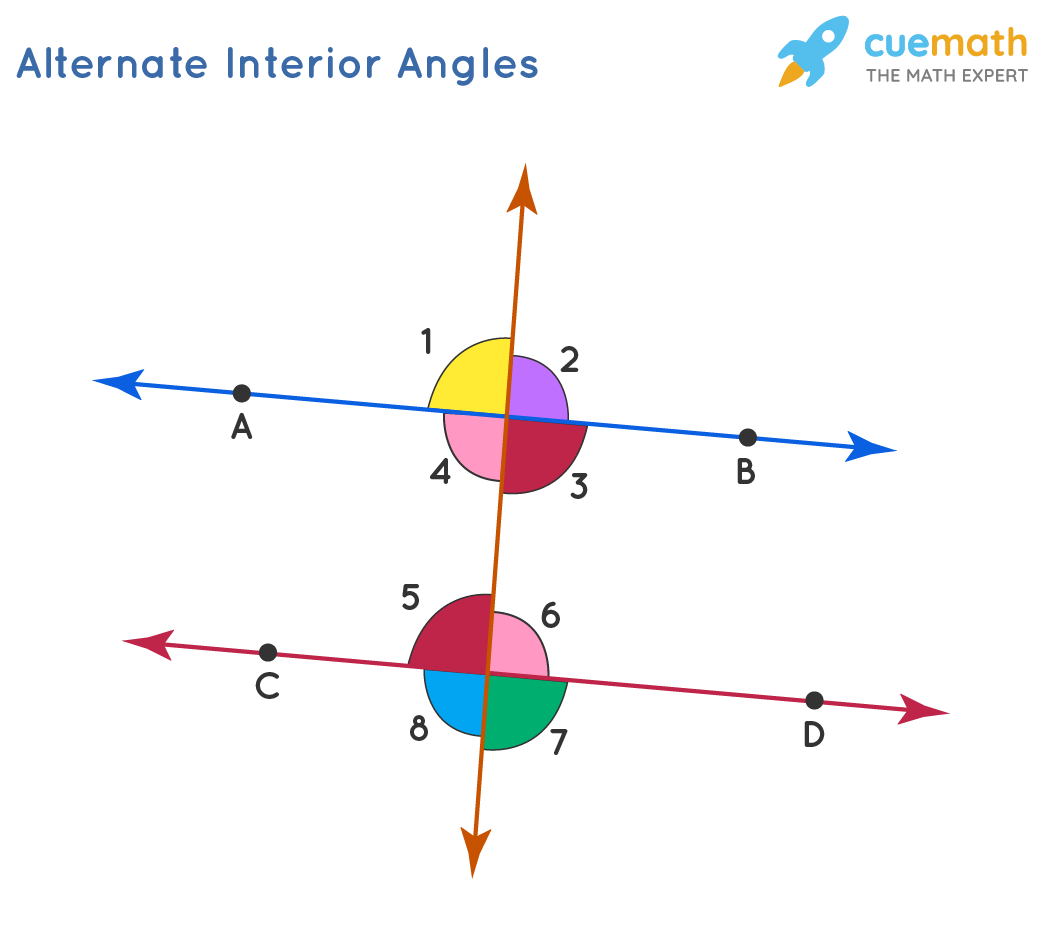
Alternate Interior Angles Definition Theorems Examples Alternate interior angles examples. example 1: find the measure of angle x in the following figure if the two lines are parallel and they are crossed by a transversal. solution: by the alternate interior angles theorem, x and 20° are the alternate interior angles. hence, they are equal. According to the image below: alternate interior angles are: ∠3 and ∠6, ∠4 and ∠5. alternate exterior angles are: ∠1 and ∠8, ∠2 and ∠7. for example: let us try to spot alternate interior angles in the given figure. remember the lines do not have to be always parallel for alternate angles to be formed.
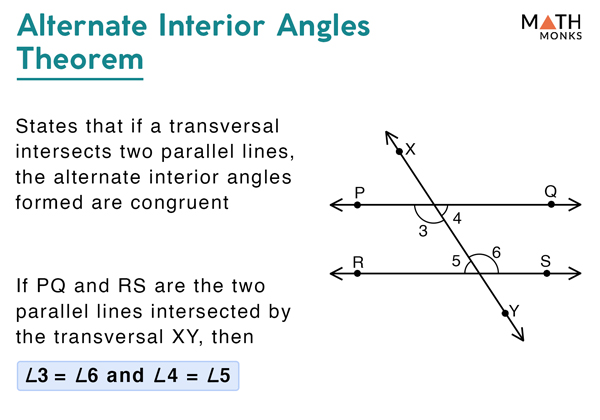
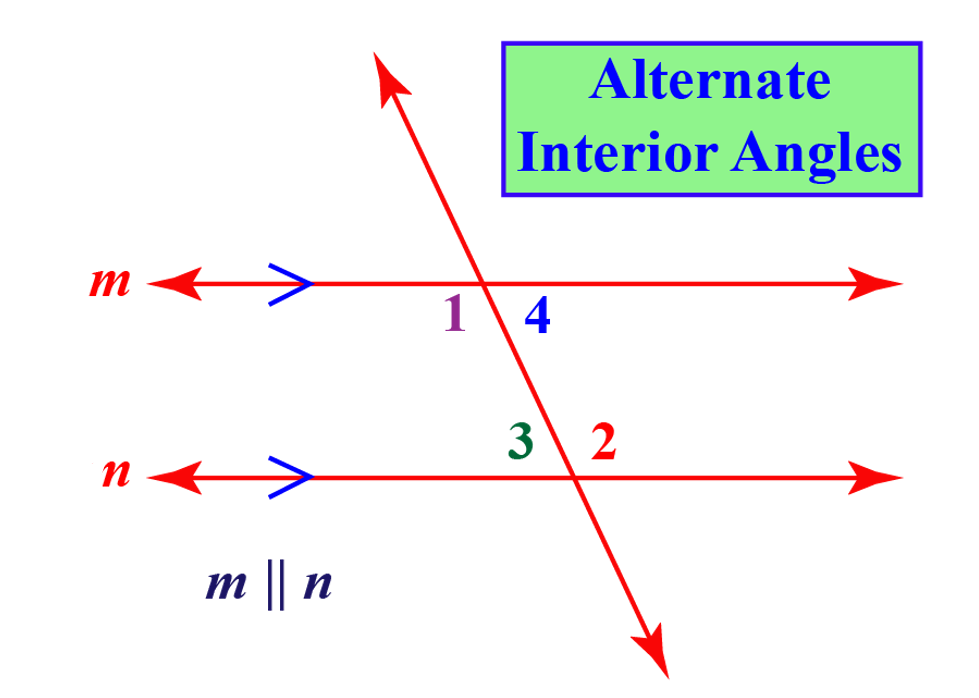
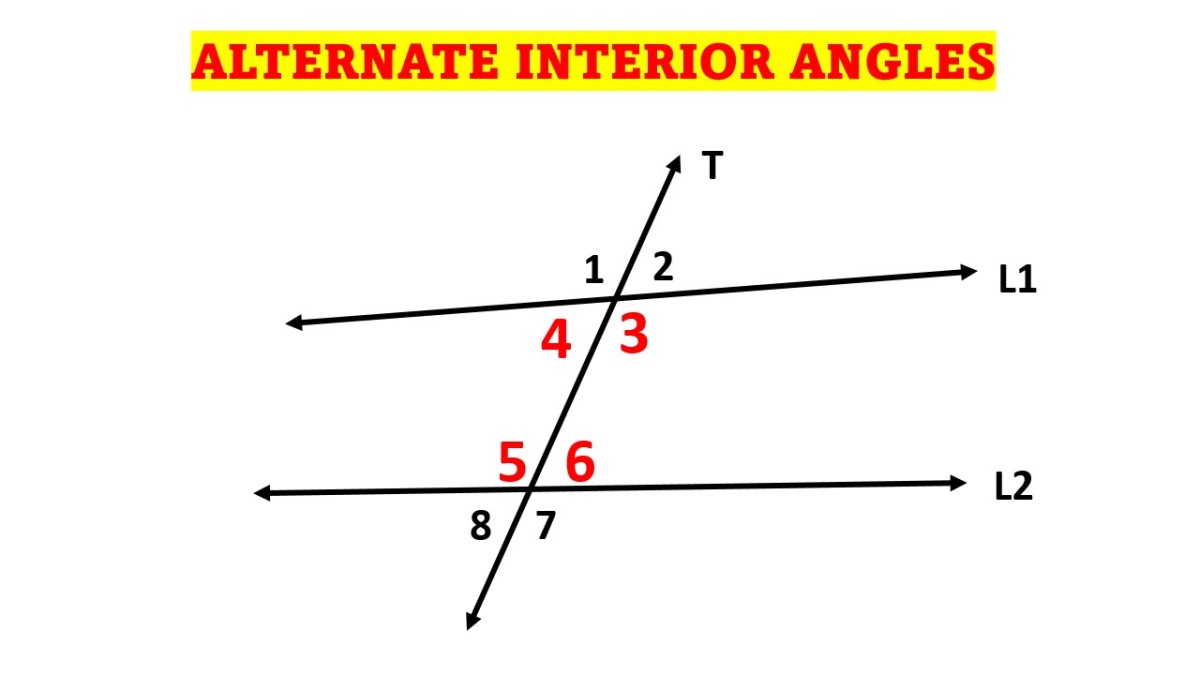
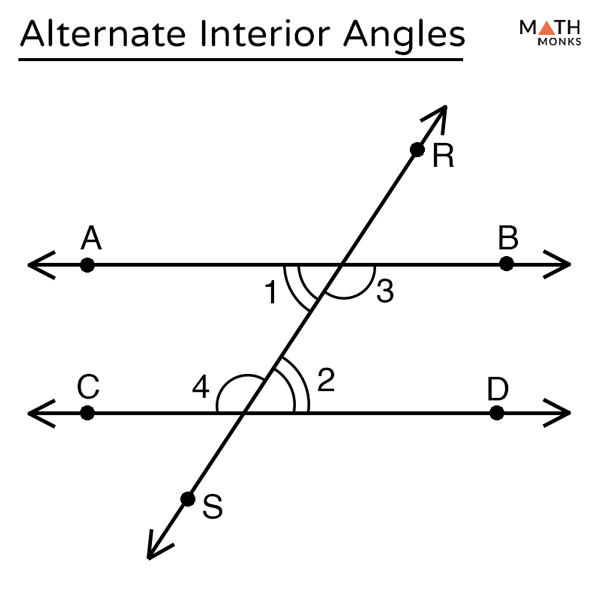
Alternate Interior Angles Definition Theorems Examples The angles which are formed inside the two parallel lines, when intersected by a transversal, are equal to its alternate pairs. these angles are called alternate interior angles. in the above given figure, you can see, two parallel lines are intersected by a transversal. therefore, the alternate angles inside the parallel lines will be equal. The following diagram shows alternate interior angles formed in two cases: i) parallel lines cut by a transversal. ii) non parallel lines cut by a transversal. alternate interior angles are: ∠2 and ∠3. ∠1 and ∠4. if the lines are parallel, the alternate interior angles are always equal. in other words, the alternate interior angles can. Alternate interior angles. when two lines are crossed by another line (called the transversal): alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. in this example c and f are a pair of alternate interior angles. also d and e are a pair of alternate interior. Solution: according to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines. thus, (4x – 19)° = (3x 16)°. 4x – 3x = 16 19. x = 35°. now, substituting the value of x in both the interior angles expression we get, (4x – 19)° = 4 x 35 – 19 = 121°. (3x 16)° = 3 x 35 16.
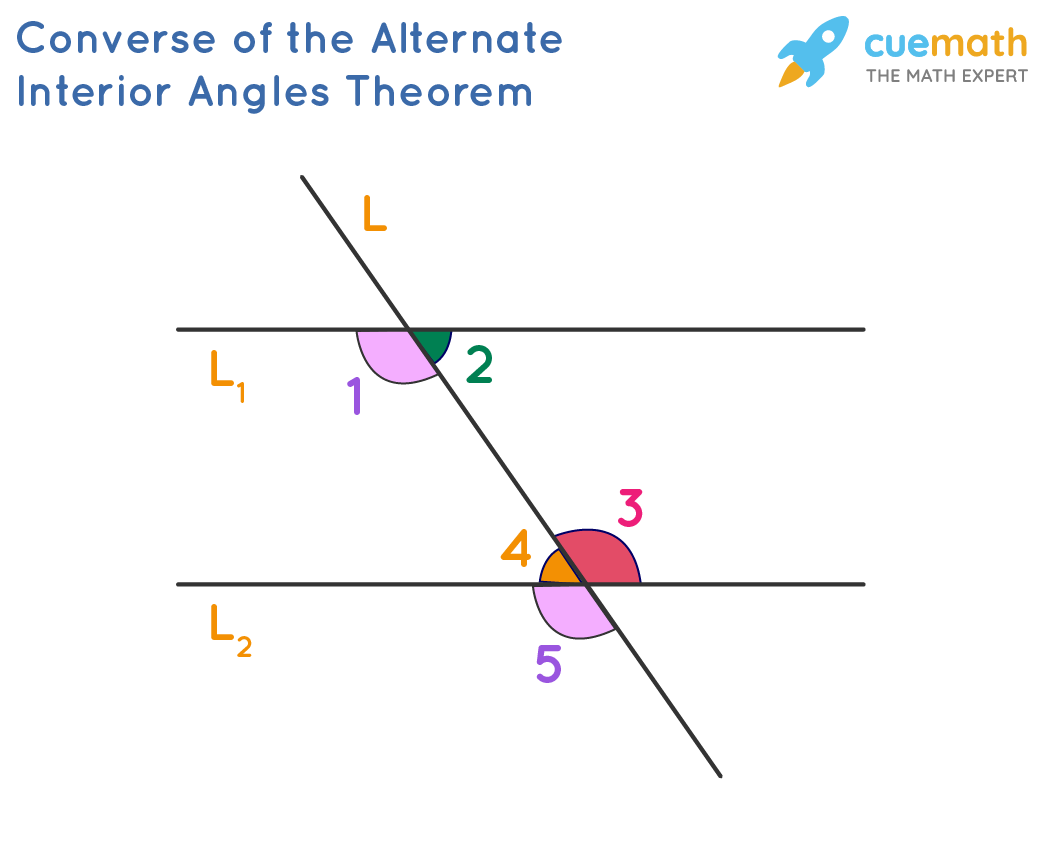
Alternate Interior Angles Definition Theorem With Examples Alternate interior angles. when two lines are crossed by another line (called the transversal): alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. in this example c and f are a pair of alternate interior angles. also d and e are a pair of alternate interior. Solution: according to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines. thus, (4x – 19)° = (3x 16)°. 4x – 3x = 16 19. x = 35°. now, substituting the value of x in both the interior angles expression we get, (4x – 19)° = 4 x 35 – 19 = 121°. (3x 16)° = 3 x 35 16. Alternate interior angles example. ∠lar is an alternate interior angle with ∠arn. ∠iar is an alternate interior angle with ∠aro. alternate interior angles theorem. the alternate interior angles theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 1. use the alternate interior angles theorem to determine if the lines cut by the transversal are parallel. solution: angle a and the angle measuring 60 ∘ form a straight angle. thus, m ∠ a 60 ∘ = 180 ∘. m ∠ a = 120 ∘. similarly, ∠ b and 120 ∘ form a straight angle, so we know that. m ∠ b 120 = 180. m ∠ b = 60 ∘.
Alternate Interior Angles Theorem Cuemath Alternate interior angles example. ∠lar is an alternate interior angle with ∠arn. ∠iar is an alternate interior angle with ∠aro. alternate interior angles theorem. the alternate interior angles theorem states that if two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 1. use the alternate interior angles theorem to determine if the lines cut by the transversal are parallel. solution: angle a and the angle measuring 60 ∘ form a straight angle. thus, m ∠ a 60 ∘ = 180 ∘. m ∠ a = 120 ∘. similarly, ∠ b and 120 ∘ form a straight angle, so we know that. m ∠ b 120 = 180. m ∠ b = 60 ∘.
Alternate Interior Angles Examples Definition Theorem Education Tips
Alternate Interior Angles Definition Theorem With Examples

Comments are closed.