Alternate Interior Angles Cuemath

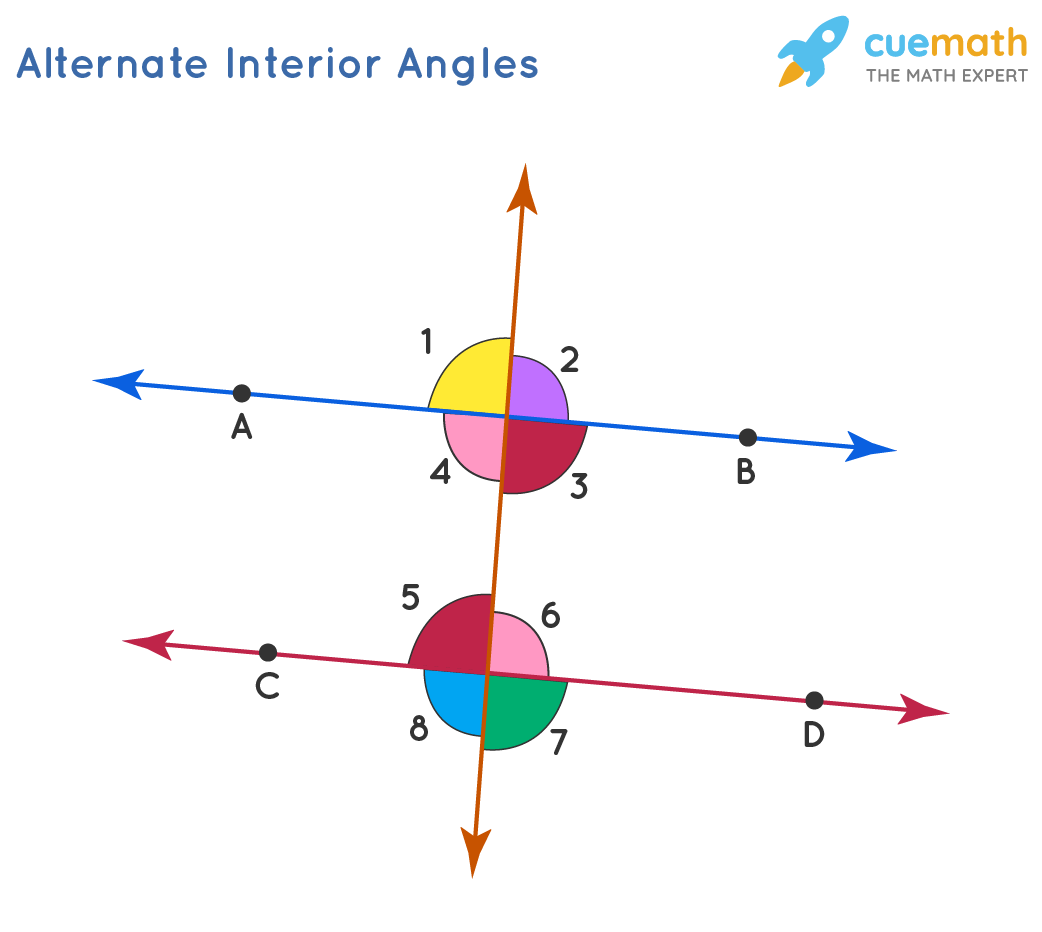
Alternate Interior Angles Cuemath Alternate interior angles examples. example 1: find the measure of angle x in the following figure if the two lines are parallel and they are crossed by a transversal. solution: by the alternate interior angles theorem, x and 20° are the alternate interior angles. hence, they are equal. According to the image below: alternate interior angles are: ∠3 and ∠6, ∠4 and ∠5. alternate exterior angles are: ∠1 and ∠8, ∠2 and ∠7. for example: let us try to spot alternate interior angles in the given figure. remember the lines do not have to be always parallel for alternate angles to be formed.

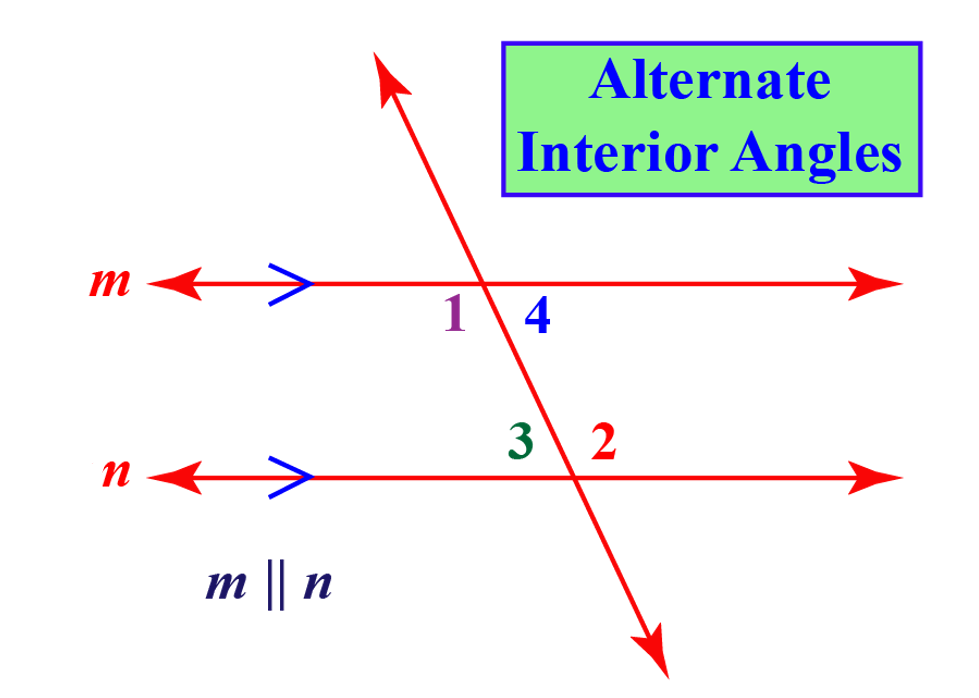
Alternate Interior Angles Theorem Cuemath Alternate angles are obtained on the opposite sides of a transversal line that have the same size. these angles are equal and are of two different types, namely alternate interior angles and alternate exterior angles. usually, interior alternate angles can be identified when a z like shape is drawn. Alternate interior angles. when two lines are crossed by another line (called the transversal): alternate interior angles are a pair of angles on the inner side of each of those two lines but on opposite sides of the transversal. in this example c and f are a pair of alternate interior angles. also d and e are a pair of alternate interior. Alternate interior angles are formed when a transversal crosses two parallel or non parallel lines. one way to help you identify this angle pair is to look closely at the words alternate and interior. in our diagram above, both are located on the inner side or in between the lines . they are also on opposite sides of the transversal and are not. Alternate interior angles are two angles that are on the interior of \(l\) and \(m\), but on opposite sides of the transversal. figure \(\pageindex{1}\) alternate interior angles theorem: if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. figure \(\pageindex{2}\).

Alternate Interior Angles Definition Theorems Examples Alternate interior angles are formed when a transversal crosses two parallel or non parallel lines. one way to help you identify this angle pair is to look closely at the words alternate and interior. in our diagram above, both are located on the inner side or in between the lines . they are also on opposite sides of the transversal and are not. Alternate interior angles are two angles that are on the interior of \(l\) and \(m\), but on opposite sides of the transversal. figure \(\pageindex{1}\) alternate interior angles theorem: if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. figure \(\pageindex{2}\). Solution: according to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines. thus, (4x – 19)° = (3x 16)°. 4x – 3x = 16 19. x = 35°. now, substituting the value of x in both the interior angles expression we get, (4x – 19)° = 4 x 35 – 19 = 121°. (3x 16)° = 3 x 35 16. The angles 4 and 5 are alternate interior angles. alternate interior angles are congruent, so set their measures equal to each other and solve for x. 5x 80 = 2x 5. 3x 80 = 5. 3x = 75. x = 25. d. angles 3 and 6 are alternate interior angles.

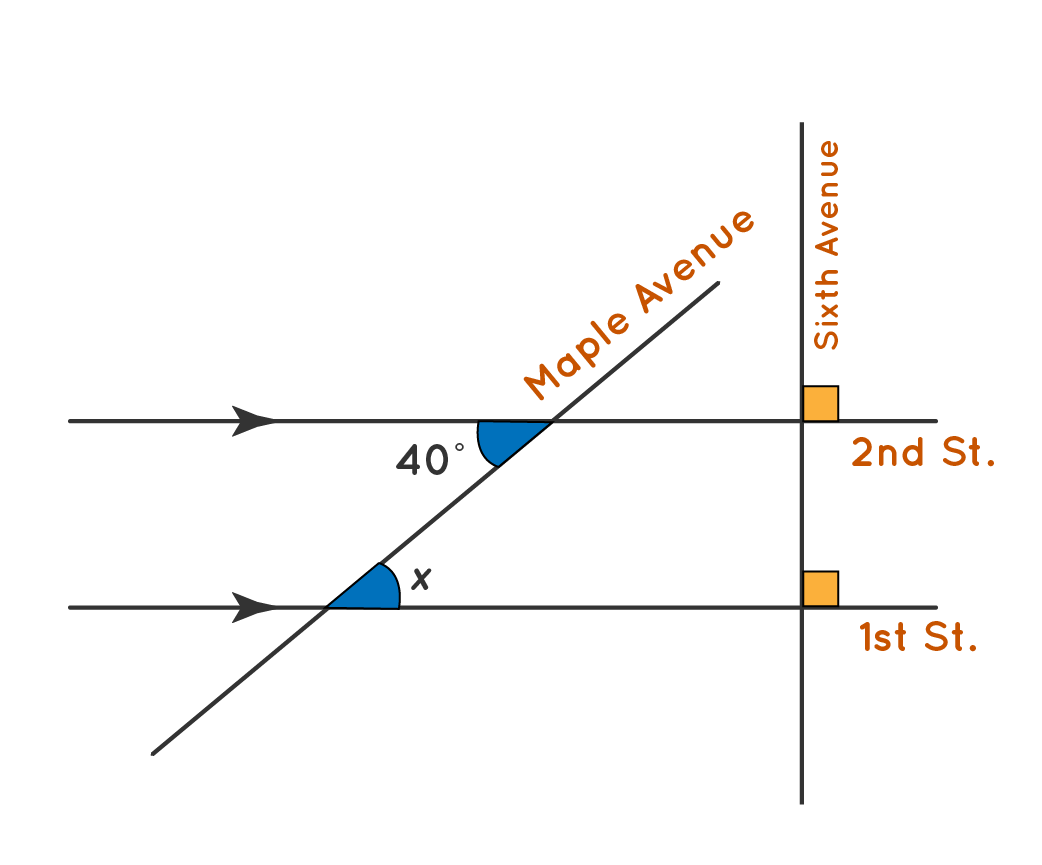
Alternate Interior Angles Definition Theorems Examples Solution: according to the interior angle theorem, alternate interior angles are equal when the transversal crosses two parallel lines. thus, (4x – 19)° = (3x 16)°. 4x – 3x = 16 19. x = 35°. now, substituting the value of x in both the interior angles expression we get, (4x – 19)° = 4 x 35 – 19 = 121°. (3x 16)° = 3 x 35 16. The angles 4 and 5 are alternate interior angles. alternate interior angles are congruent, so set their measures equal to each other and solve for x. 5x 80 = 2x 5. 3x 80 = 5. 3x = 75. x = 25. d. angles 3 and 6 are alternate interior angles.