A Visual Introduction To The Zernike Polynomials

A Visual Introduction To The Zernike Polynomials Youtube The zernike polynomials are very useful functions with broad applications. these polynomials have the special property that they form an orthonormal basis in. Zernike polynomials 1 introduction often, to aid in the interpretation of optical test results it is convenient to express wavefront data in polynomial form. zernike polynomials are often used for this purpose since they are made up of terms that are of the same form as the types of aberrations often observed in optical tests (zernike, 1934).

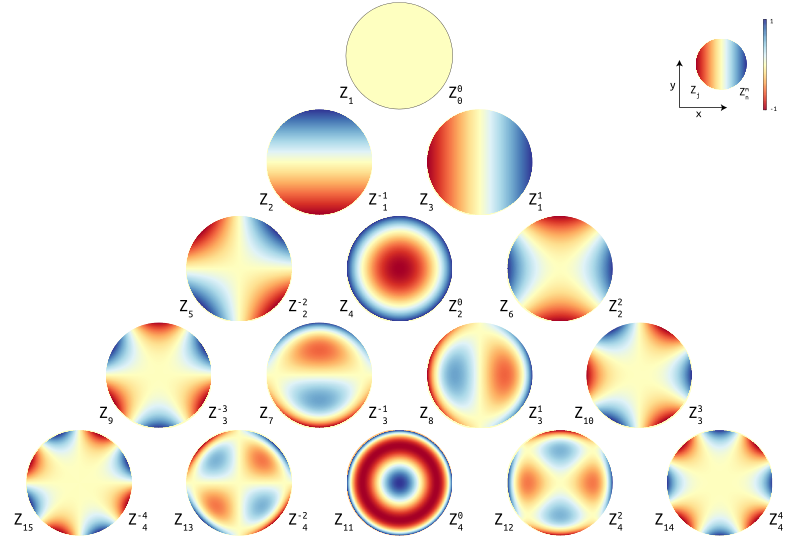
Zernike Polynomials Zernike polynomials have the property of being limited to a range of −1 to 1, i.e. . the radial polynomials are defined as. for an even number of n − m, while it is 0 for an odd number of n − m. a special value is. Description of zernike polynomials jim schwiegerling. the zernike polynomials are a set of functions that are orthogonal over the unit circle. they are useful for describing the shape of an aberrated wavefront in the pupil of an optical system or true height corneal topography. there exist several different normalization and numbering schemes. Zernike polynomials: a guide. april 2011; introduction. the zernike polynomials are a sequence of polyno visual ophthalmic optics; it is nothing but the ordinary. Zernike polynomials • at least six different schemes exist for the zernike polynomials. • some schemes only use a single index number instead of n and m. with the single number, there is no unique ordering or definition for the polynomials, so different orderings are used. • some schemes set the normalization to unity for all polynomials.

Color Map Diagram Of Zernike Polynomials Up To The 4th Order Astig 45 Zernike polynomials: a guide. april 2011; introduction. the zernike polynomials are a sequence of polyno visual ophthalmic optics; it is nothing but the ordinary. Zernike polynomials • at least six different schemes exist for the zernike polynomials. • some schemes only use a single index number instead of n and m. with the single number, there is no unique ordering or definition for the polynomials, so different orderings are used. • some schemes set the normalization to unity for all polynomials. Keywords: optical aberrations; zernike polynomials; special functions; aberrometry. 1. introduction. the zernike polynomials are a sequence of polyno mials that are continuous and orthogonal over a unit circle. a large fraction of optical systems in use today employ imaging elements and pupils which are circu lar. Building on all of the previous zernike polynomials before it. in other words, using the gram schmidt orthogonalization process one cannot get the nth zernike polynomial without first obtaining all the zernike polynomials of {n 1, n 2, …, 1}. thus the gram schmidt orthogonalization process can become cumbersome in the pursuit of high order.

The First 15 Zernike Polynomials 22 Download Scientific Diagram Keywords: optical aberrations; zernike polynomials; special functions; aberrometry. 1. introduction. the zernike polynomials are a sequence of polyno mials that are continuous and orthogonal over a unit circle. a large fraction of optical systems in use today employ imaging elements and pupils which are circu lar. Building on all of the previous zernike polynomials before it. in other words, using the gram schmidt orthogonalization process one cannot get the nth zernike polynomial without first obtaining all the zernike polynomials of {n 1, n 2, …, 1}. thus the gram schmidt orthogonalization process can become cumbersome in the pursuit of high order.

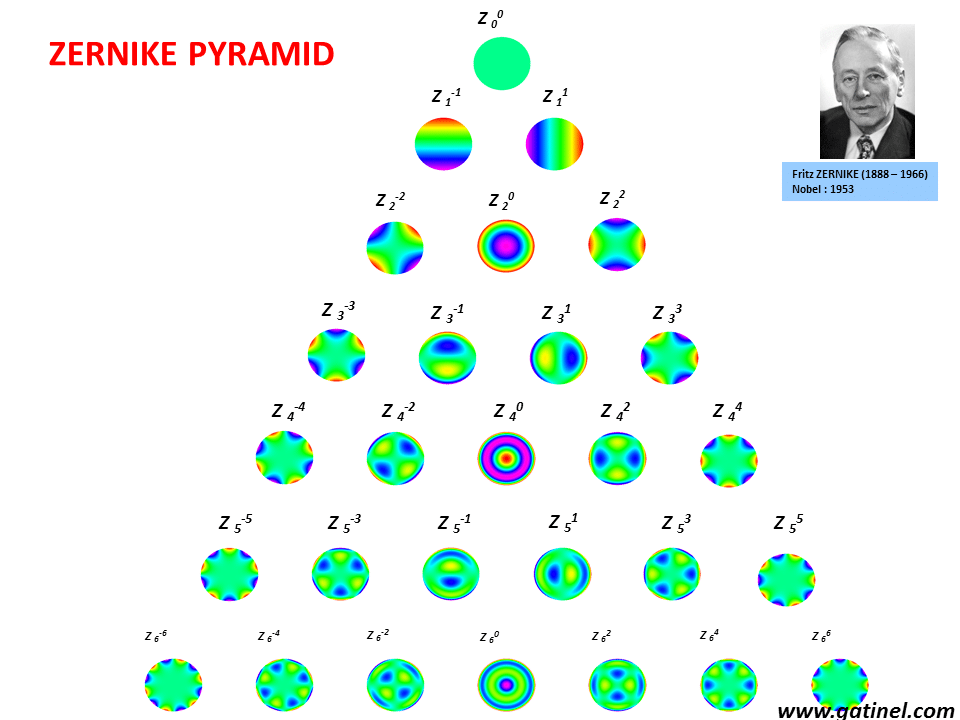
Zernike Polynomials Docteur Damien Gatinel