A Simple Proof Of The Pythagorean Theorem Download Scientific Diagram

A Simple Proof Of The Pythagorean Theorem Download Scientific Diagram Download scientific diagram | a proof of the pythagorean theorem from publication: visually dynamic presentation of proofs in plane geometry: part 1. basic features and the manual input method. Download scientific diagram | a simple proof of the pythagorean theorem. from publication: pythagoras: everyone knows his famous theorem, but not who discovered it 1000 years before him | everyone.

Visual Representation Of A Proof Of Pythagorean Theorem Download Proof by rearrangement. pythagoras's proof. given any right triangle with legs a a and b b and hypotenuse c c like the above, use four of them to make a square with sides a b a b as shown below: this forms a square in the center with side length c c and thus an area of c^2. c2. however, if we rearrange the four triangles as follows, we can see. Some popular dissection proofs of the pythagorean theorem such as proof #36 on cut the knot demonstrate a specific, clear pattern for cutting up the figure's three squares, a pattern that applies to all right triangles. i have yet to find a similarly straightforward cutting pattern that would apply to all triangles and show that my same. Th 20 feet and length 21 feet. let’s plug these values into th. pythagorean theorem equation. if the equation holds, the triangle is a right triangle; if it does not hold, this tr. (leg1)2 (leg2)2 = (hypotenuse)2. t2 = 841 ft2 841 ft2 = 841 ft2we can conclude that the triangle is a right triangle because both s. Download scientific diagram | very simple proofs using the given triangle directly from publication: a new approach to proving the pythagorean theorem c k shene | ne'kiya d. jackson and calcea.

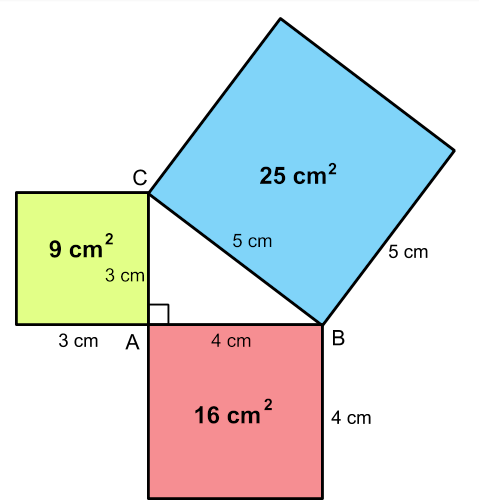
Euclid S Proof Of The Pythagorean Theorem Download Scientific Diagram Th 20 feet and length 21 feet. let’s plug these values into th. pythagorean theorem equation. if the equation holds, the triangle is a right triangle; if it does not hold, this tr. (leg1)2 (leg2)2 = (hypotenuse)2. t2 = 841 ft2 841 ft2 = 841 ft2we can conclude that the triangle is a right triangle because both s. Download scientific diagram | very simple proofs using the given triangle directly from publication: a new approach to proving the pythagorean theorem c k shene | ne'kiya d. jackson and calcea. The pythagorean theorem describes the relationship between the side lengths of right triangles. the diagram shows a right triangle with squares built on each side. if we add the areas of the two small squares, we get the area of the larger square. the square of the hypotenuse is equal to the sum of the squares of the legs. Visual proof. the visual proof is quite simple. we form a square using four identical triangles, like this: the outer square has sides of length a b. the inner square (the yellow area) is a square whose sides have length c because each side of the square is made from the hypotenuse of one of the triangles, which we previously said has length c:.

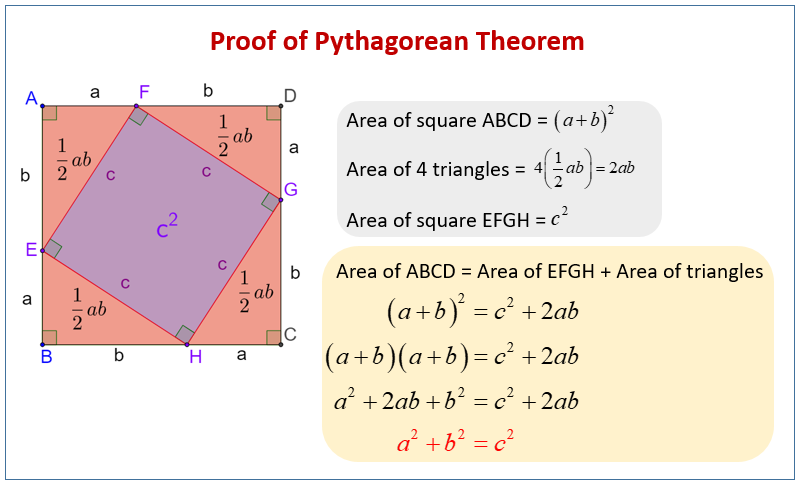
Proving The Pythagorean Theorem Math Liberty The pythagorean theorem describes the relationship between the side lengths of right triangles. the diagram shows a right triangle with squares built on each side. if we add the areas of the two small squares, we get the area of the larger square. the square of the hypotenuse is equal to the sum of the squares of the legs. Visual proof. the visual proof is quite simple. we form a square using four identical triangles, like this: the outer square has sides of length a b. the inner square (the yellow area) is a square whose sides have length c because each side of the square is made from the hypotenuse of one of the triangles, which we previously said has length c:.

The Pythagorean Theorem Math Tutor Free Math For All

Proof Of The Pythagoras Theorem Own Representation Download