A Proof That The Square Root Of Two Is Irrational
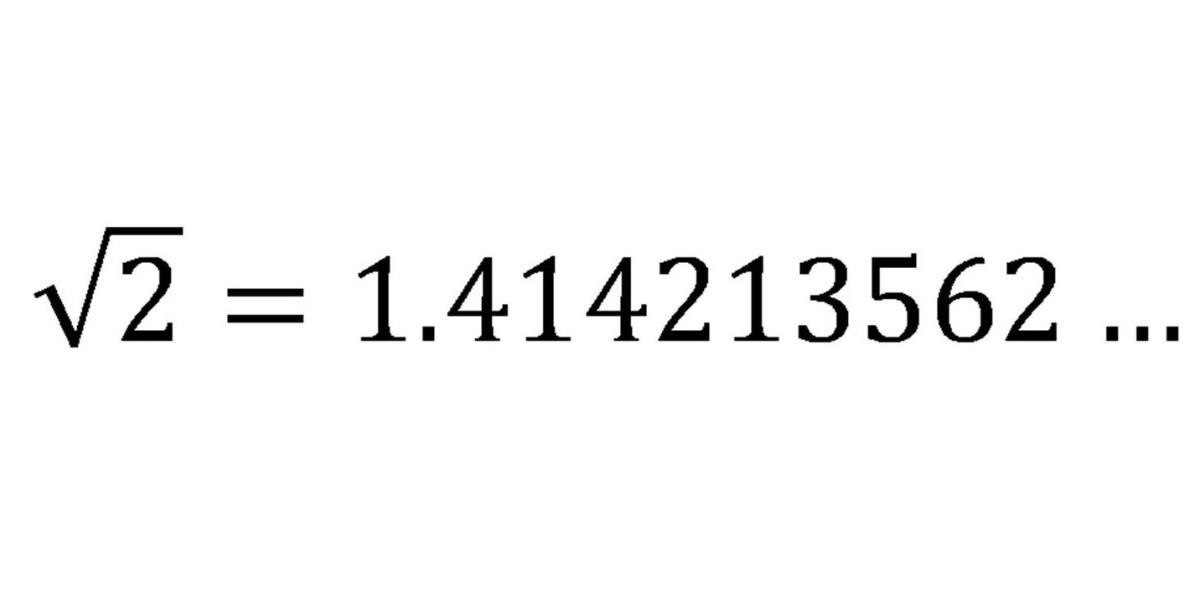
How To Prove That The Square Root Of 2 Is Irrational Owlcation Euclid proved that √2 (the square root of 2) is an irrational number. he used a proof by contradiction. first euclid assumed √2 was a rational number. a rational number is a number that can be in the form p q where p and q are integers and q is not zero. he then went on to show that in the form p q it can always be simplified. The irrationality of the square root of 2 follows from our knowledge of how pythagorean triples behave, specifically, that for positive integers x, y, and z, if x^2 y^2 = z^2, then x is not equal to y. but if the square root of 2 were rational, then there would exist positive integers a and b such that a b = the square root of 2. then a^2 b^2.

How To Prove That Square Root 2 Is An Irrational Number A Quick Maths A proof that the square root of 2 is irrational. let's suppose √ 2 is a rational number. then we can write it √ 2 = a b where a, b are whole numbers, b not zero. we additionally assume that this a b is simplified to lowest terms, since that can obviously be done with any fraction. notice that in order for a b to be in simplest terms, both. The square root of two forms the relationship of f stops in photographic lenses, which in turn means that the ratio of areas between two successive apertures is 2. the celestial latitude (declination) of the sun during a planet's astronomical cross quarter day points equals the tilt of the planet's axis divided by 2 {\displaystyle {\sqrt {2}}} . Prove: the square root of [latex]2[ latex], [latex]sqrt 2 [ latex], is irrational. proving that [latex]color{red}{sqrt2}[ latex] is irrational is a popular example used in many textbooks to highlight the concept of proof by contradiction (also known as indirect proof). this proof technique is simple yet elegant and powerful. basic steps involved in the proof by contradiction: brainstorm. Proof 5. by the rational root theorem, every rational root of the polynomial n2 − 2 would have a numerator that divides 2 and a denominator that divides 1, i.e., the only possible rational roots: n = ± 1, ± 2. but (± 1)2 − 2 ≠ 0 ≠ (± 2)2 − 2. so, its root n = √2 is not a rational number.
Prove That Square Root Of 2 Is Irrational Prove: the square root of [latex]2[ latex], [latex]sqrt 2 [ latex], is irrational. proving that [latex]color{red}{sqrt2}[ latex] is irrational is a popular example used in many textbooks to highlight the concept of proof by contradiction (also known as indirect proof). this proof technique is simple yet elegant and powerful. basic steps involved in the proof by contradiction: brainstorm. Proof 5. by the rational root theorem, every rational root of the polynomial n2 − 2 would have a numerator that divides 2 and a denominator that divides 1, i.e., the only possible rational roots: n = ± 1, ± 2. but (± 1)2 − 2 ≠ 0 ≠ (± 2)2 − 2. so, its root n = √2 is not a rational number. "the square root of 2 is irrational" it is thought to be the first irrational number ever discovered. but there are lots more. reductio ad absurdum. by the way, the method we used to prove this (by first making an assumption and then seeing if it works out nicely) is called "proof by contradiction" or "reductio ad absurdum". Practice this lesson yourself on khanacademy.org right now: khanacademy.org math algebra rational and irrational numbers irrational numbers e reco.

Proof Square Root Of 2 Is Irrational Youtube "the square root of 2 is irrational" it is thought to be the first irrational number ever discovered. but there are lots more. reductio ad absurdum. by the way, the method we used to prove this (by first making an assumption and then seeing if it works out nicely) is called "proof by contradiction" or "reductio ad absurdum". Practice this lesson yourself on khanacademy.org right now: khanacademy.org math algebra rational and irrational numbers irrational numbers e reco.

Prove That Root 2 Is Irrational Teachoo With Video Examples

Square Root Of 2 Is Irrational Unlocking The Mystery With A

Comments are closed.