A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie
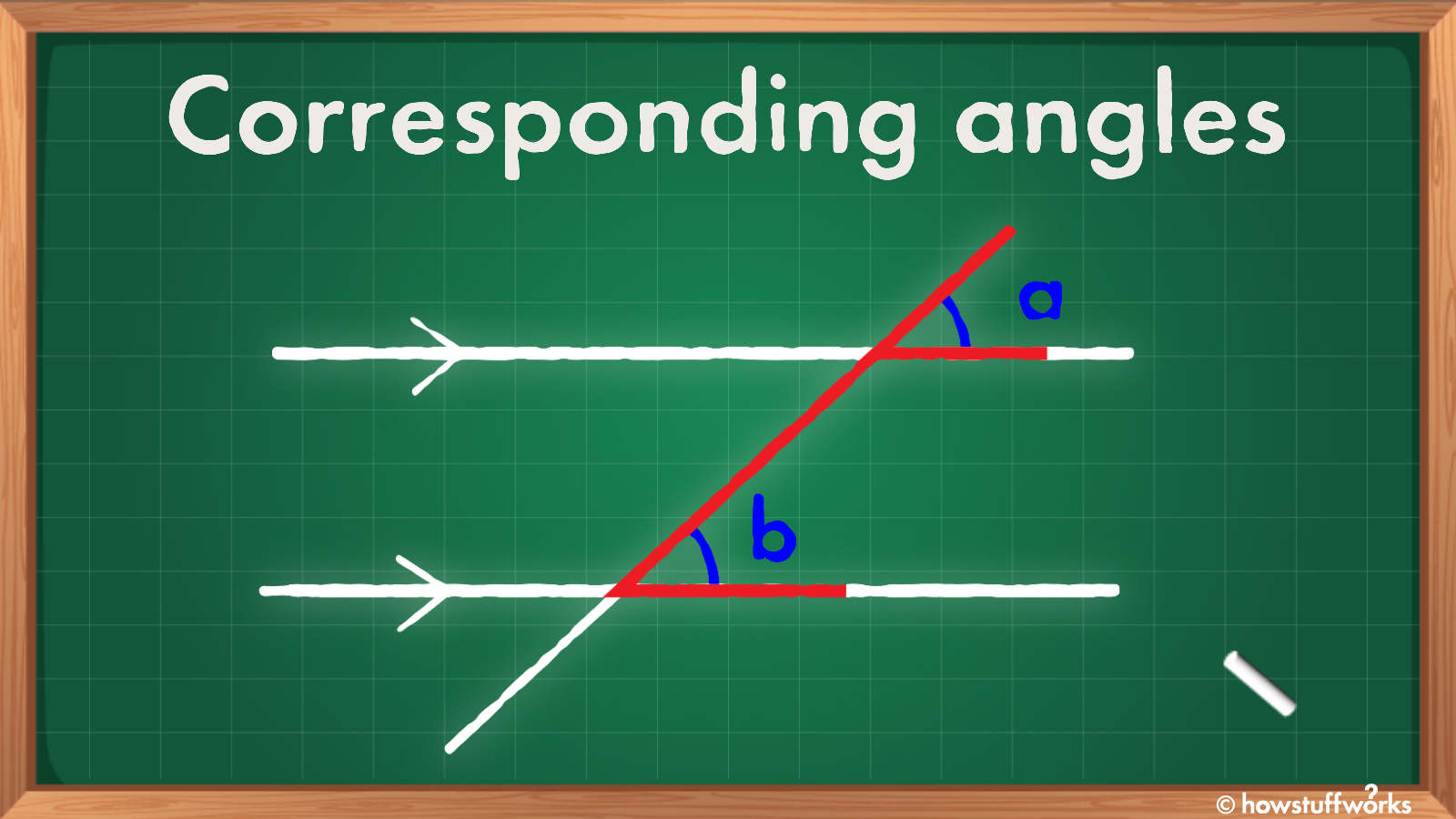
A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie Corresponding angles are pairs of angles that occupy the same relative position at each intersection when a transversal intersects two parallel straight lines. corresponding angles. the above figure shows two parallel lines ab and cd intersected by the transversal gh. the pairs of corresponding angles in the given figure are: ∠1 and ∠5. ∠. Corresponding angles in geometry are defined as the angles which are formed at corresponding corners when two parallel lines are intersected by a transversal. i.e., two angles are said to be corresponding angles if: the angles lie at different corners. they lie on the same (corresponding) side of the transversal.
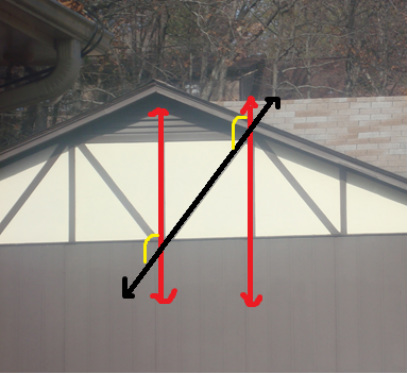
A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie Example 2: find pairs of corresponding angles. ← s→ y s y and ← t → z t z are parallel lines. name all pairs of corresponding angles. identify two parallel lines that are intersected by a transversal. show step. the two parallel lines are sy s y and t z. tz. line u x u x is the transversal. Example 3. the two corresponding angles of a figure measure 7y – 12 and 5y 6. find the magnitude of a corresponding angle. solution. first, we need to determine the value of y. the two corresponding angles are always congruent. hence, 7y – 12 = 5y 6. 7y – 5y = 12 6. 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Solution: remember, if the lines are parallel, all corresponding angles are equal. so, all the corresponding angles measure 45 degrees! example 2: two parallel lines are cut by a transversal. one of the corresponding angles measures ‘x’, and another angle on the transversal is ‘3x 10’. find the value of ‘x’.

A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie 2x = 11. x = 112. x = 5.5. 2. if eg and bd are two parallel lines, find the measure of the angle x. solution: the angles ∠gfh and ∠efc are vertically opposite angles. vertical angles are always congruent. thus, m∠cfe = m∠gfh = 48°. now, the angles ∠efc and ∠bca are corresponding angles formed by parallel lines. Solution: remember, if the lines are parallel, all corresponding angles are equal. so, all the corresponding angles measure 45 degrees! example 2: two parallel lines are cut by a transversal. one of the corresponding angles measures ‘x’, and another angle on the transversal is ‘3x 10’. find the value of ‘x’. Example 3: the values of two corresponding angles ∠1 = 3x 1 and ∠5 = 4x – 3. solve for the value of x. answer: as they are corresponding angles and the lines are said to be parallel in nature, then they should be congruent. equate the given expressions ∠1 = 3x 1 and ∠5 = 4x – 3 and find the value of x. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles.
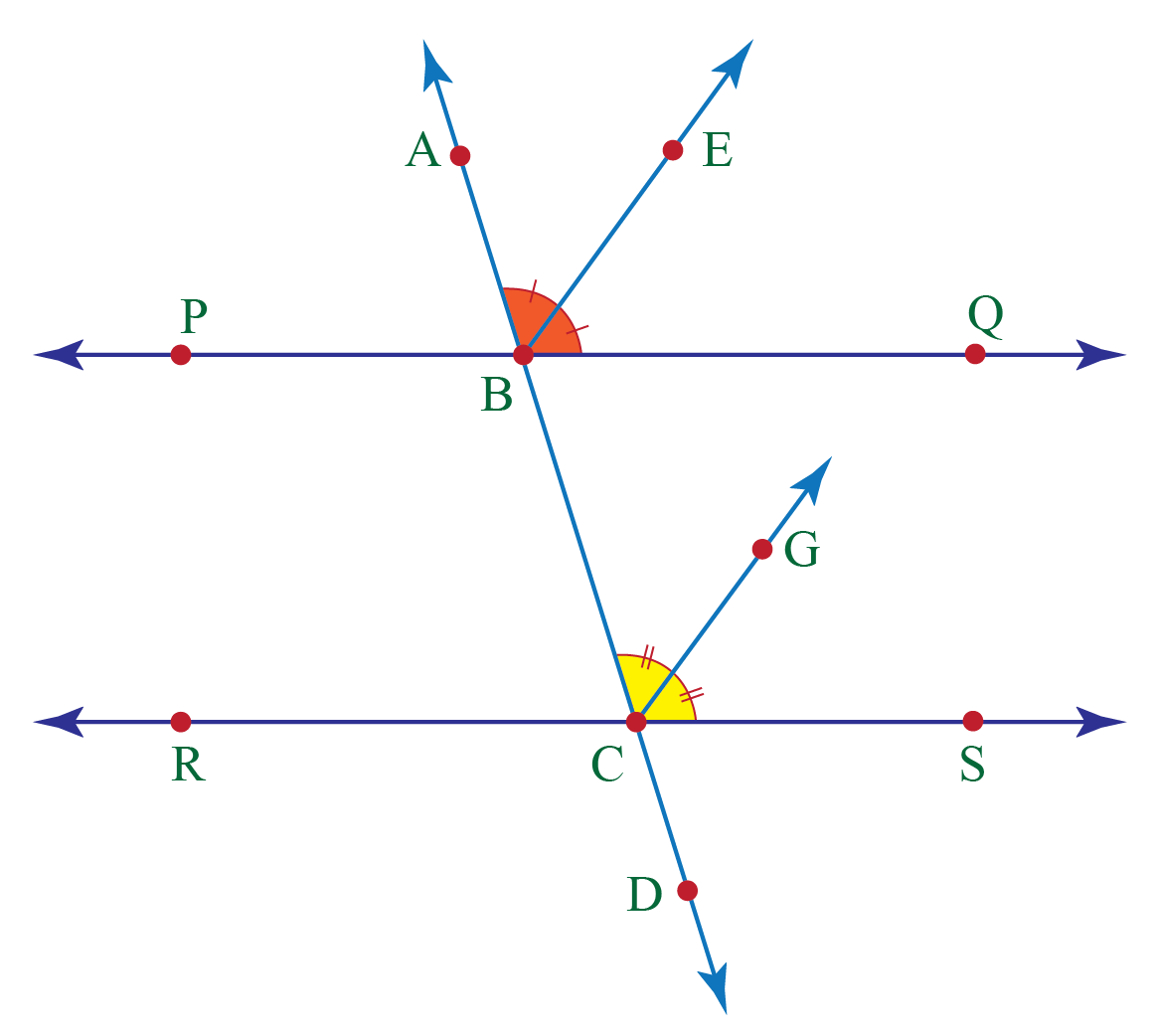
A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie Example 3: the values of two corresponding angles ∠1 = 3x 1 and ∠5 = 4x – 3. solve for the value of x. answer: as they are corresponding angles and the lines are said to be parallel in nature, then they should be congruent. equate the given expressions ∠1 = 3x 1 and ∠5 = 4x – 3 and find the value of x. Corresponding angles are two angles that lie in similar relative positions on the same side of a transversal or at each intersection. they are usually formed when two parallel or non parallel lines are cut by a transversal. in our illustration above, parallel lines are cut by a transversal which as a result, formed 4 corresponding angles.
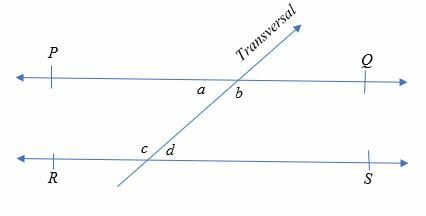
A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie

A Pair Of Corresponding Angles In Real Life Examples Kropkowe Kocie

Comments are closed.