A Neat Radical Equation Relating The Radii Of Three Circles Tangent To Each Other

A Neat Radical Equation Relating The Radii Of Three Circles Tangent To In this video, i showed how to derive the equation 1 sqrt(c) = 1 sqrt(a) 1 sqrt(b) which relates the radii of three circles externally tangent to one anoth. Learn to apply systems of equations in solving geometry problems. how to find the radii of three circles touching each other externally or externally tangent.

Prove An Equation On Radii Of 3 Tangent Circles Geometry 1. in mr. michael rozenberg‘s post, we can easily get the radius r cm of the circle inscribed by the three circles tangent to each other. r = 6 23 first of all, we know that the equations of the circles with radii 1 and 3 are respectively c1: x2 y2 = 1 and c3: (x − 3)2 y2 = 4 now we dilate the circle (as shown below) c1 and c3 by. Three circles with radii 1, 2, and 3 ft. are externally tangent to one another, as shown in the figure. find the area of the sector of the circle of radius 1 ft. that is cut off by the line segments joining the center of that circle to the centers of the other two circles. the length of the sides of a triangle is calculated by the sum of the. Question 388452: three circles of radii 2, 4, and 6 are tangent to each other externally. find the area of the triangle formed by connecting their centers. answer by fombitz(32388) (show source):. Circles of radius and are externally tangent to each other and are internally tangent to a circle of radius . the circle of radius has a chord that is a common external tangent of the other two circles. find the square of the length of this chord. solution 1. we label the points as following: the centers of the circles of radii are respectively.

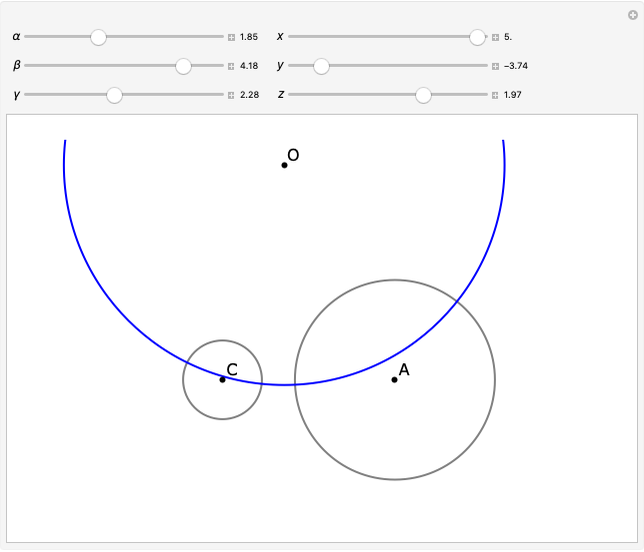
Radical Circle Of Three Circles Wolfram Demonstrations Project Question 388452: three circles of radii 2, 4, and 6 are tangent to each other externally. find the area of the triangle formed by connecting their centers. answer by fombitz(32388) (show source):. Circles of radius and are externally tangent to each other and are internally tangent to a circle of radius . the circle of radius has a chord that is a common external tangent of the other two circles. find the square of the length of this chord. solution 1. we label the points as following: the centers of the circles of radii are respectively. The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". Tangent circles. download wolfram notebook. two circles with centers at with radii for are mutually tangent if. (1) if the center of the second circle is inside the first, then the and signs both correspond to internally tangent circles. if the center of the second circle is outside the first, then the sign corresponds to externally tangent.

Three Circles Of Radii A B And C Touch Each Other Externally If They The radius of circle a is equal to 10 cm and the radius of circle b is equal to 8 cm. find the radius of circle c. solution to problem. let a, b and c be the radii of the three circles. we first draw the lines aa', bb' and cc' perpendicular to line l. b'c, ca' and ba" are parallel to line l. let x = b'c, y=a'c and z = ba". Tangent circles. download wolfram notebook. two circles with centers at with radii for are mutually tangent if. (1) if the center of the second circle is inside the first, then the and signs both correspond to internally tangent circles. if the center of the second circle is outside the first, then the sign corresponds to externally tangent.