A Fibonacci Sequence Oya Fibonacci 50 Off
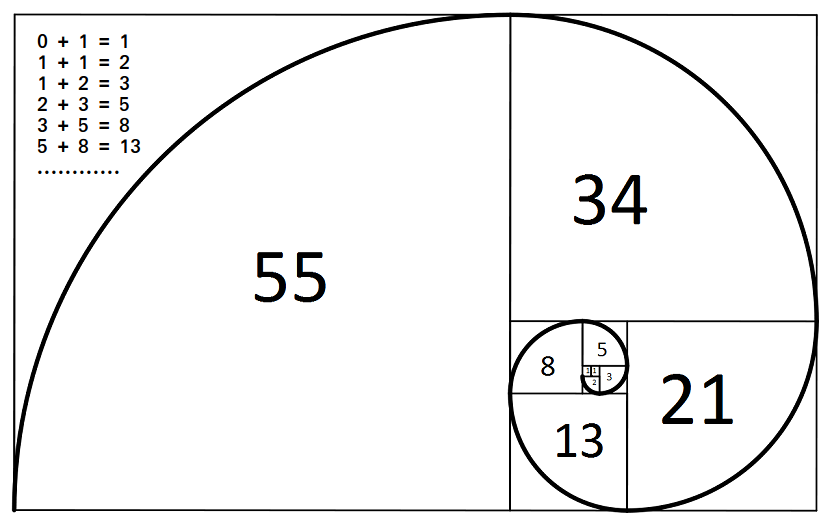
Fibonacci数列 斐波那契数列的归递returnfab N 1 Fab N 2 Csdn博客 In mathematics, the fibonacci numbers form a sequence such that each number is the sum of the two preceding numbers, starting from 0 and 1. that is f n = f n 1 f n 2, where f 0 = 0, f 1 = 1, and n≥2. the sequence formed by fibonacci numbers is called the fibonacci sequence. the following is a full list of the first 10, 100, and 300. You can also calculate a single number in the fibonacci sequence, f n, for any value of n up to n = ±500. fibonacci sequence. the fibonacci sequence is a set of numbers such that each number in the sequence is the sum of the two numbers that immediatly preceed it. \[ f {0} = 0,\quad f {1} = f {2} = 1, \] and.

Fibonacci Sequence Inforgraphic Poster Acronymat In 2024 Fibonacci sequence. in mathematics, the fibonacci sequence is a sequence in which each number is the sum of the two preceding ones. numbers that are part of the fibonacci sequence are known as fibonacci numbers, commonly denoted fn . many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 [1][2] and some (as. Fibonacci was not the first to know about the sequence, it was known in india hundreds of years before! about fibonacci the man. his real name was leonardo pisano bogollo, and he lived between 1170 and 1250 in italy. "fibonacci" was his nickname, which roughly means "son of bonacci". The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034. Here are some interesting facts about the fibonacci numbers: this sequence is called the fibonacci sequence and it's an infinite sequence. each number in the fibonacci series or sequence is represented as f n. as shown below, fib numbers can be represented as a spiral, if we make squares with those lengths. in the given figure, we can see how.

The Fibonacci Sequence Fibonacci Fibonacci Sequence Math Facts The fibonacci sequence has several interesting properties. 1) fibonacci numbers are related to the golden ratio. any fibonacci number can be calculated (approximately) using the golden ratio, f n = (Φ n (1 Φ) n) √5 (which is commonly known as "binet formula"), here φ is the golden ratio and Φ ≈ 1.618034. Here are some interesting facts about the fibonacci numbers: this sequence is called the fibonacci sequence and it's an infinite sequence. each number in the fibonacci series or sequence is represented as f n. as shown below, fib numbers can be represented as a spiral, if we make squares with those lengths. in the given figure, we can see how. Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. The fibonacci numbers are the sequence of numbers {f n} (n=1)^infty defined by the linear recurrence equation f n=f (n 1) f (n 2) (1) with f 1=f 2=1. as a result of the definition (1), it is conventional to define f 0=0. the fibonacci numbers for n=1, 2, are 1, 1, 2, 3, 5, 8, 13, 21, (oeis a000045). fibonacci numbers can be viewed as a particular case of the fibonacci polynomials f n(x.

å Fibonacci Sequence ôÿå Fibonacci 50 Off Solved examples. find the sum of the first 15 fibonacci numbers. solution: as we know, the sum of the fibonacci sequence = ∑ i = 0 n f i = f n 2 – f 2. = f n 2 − 1, where f n is the nth fibonacci number, and the sequence starts from f 0. thus, the sum of the first 15 fibonacci numbers = (15 2) th term – 2 nd term. The fibonacci numbers are the sequence of numbers {f n} (n=1)^infty defined by the linear recurrence equation f n=f (n 1) f (n 2) (1) with f 1=f 2=1. as a result of the definition (1), it is conventional to define f 0=0. the fibonacci numbers for n=1, 2, are 1, 1, 2, 3, 5, 8, 13, 21, (oeis a000045). fibonacci numbers can be viewed as a particular case of the fibonacci polynomials f n(x.

The Fibonacci Sequence All About Fibonacci
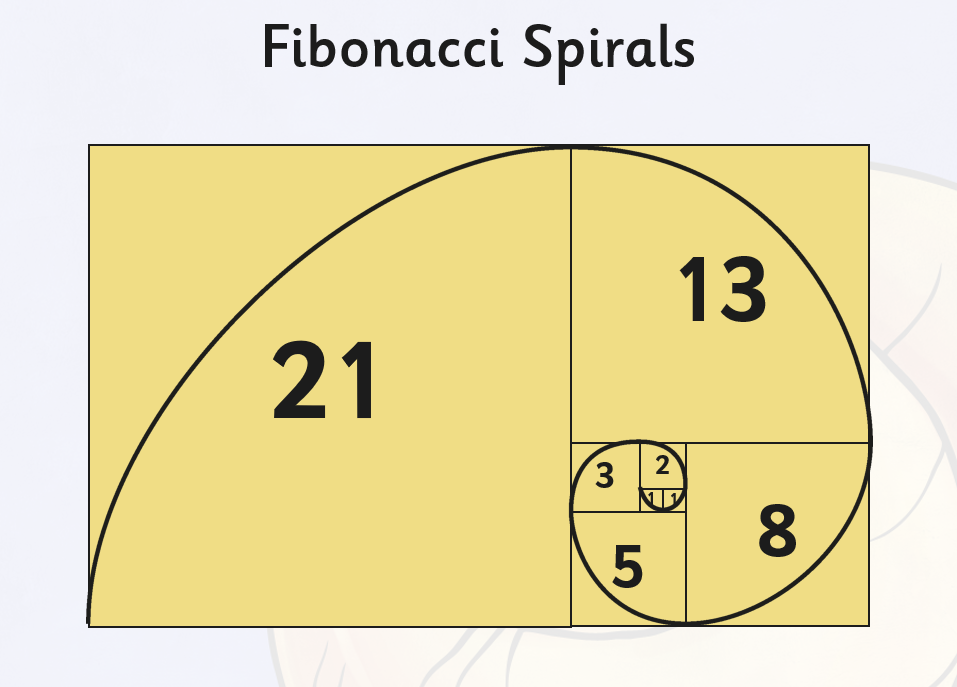
What Is The Fibonacci Sequence Answered Twinkl Teaching Wiki

Comments are closed.