8 Write The Formula To Find The Mean Using Deviation Method And
8 Write The Formula To Find The Mean Using Deviation Method And The mean deviation of the data values can be easily calculated using the below procedure. step 1: find the mean value for the given data values. step 2: now, subtract the mean value from each of the data values given (note: ignore the minus symbol) step 3: now, find the mean of those values obtained in step 2. We use the central points (mean, median, or mode) to find the mean deviation. we only use the mean to find the standard deviation. we take the absolute value of the deviations to find the mean deviation. to find the standard deviation, we use the square of the deviations. it is less frequently used.

Mean Deviation Formula Learn Formula For Mean Deviation Find the mean of all values use it to work out distances then find the mean of those distances! in three steps: 1. find the mean of all values; 2. find the distance of each value from that mean (subtract the mean from each value, ignore minus signs) 3. then find the mean of those distances; like this:. Step 4: find the sum of all the deviations and divide it by the number of observations to get the mean deviation. this can be understood using the example, example: find the mean deviation of the given data about their mean. {4, 6, 7, 3, 5, 5} solution: step 1: find the mean of the given data. Step 1 – calculate the mean, median or mode value of the given data set. step 2 – then we must find the absolute difference between each value in the data set with the mean, ignoring the signs. step 3 – we then sum up all the deviations. step 4 – finally, we find the mean or average of those values found in step 3. Step deviation method; let us go through the formulas in these three methods given below: direct method. suppose x 1, x 2, x 3,…., x n be n observations with respective frequencies f 1, f 2, f 3,…., f n. this means, the observation x 1 occurs f 1 times, x 2 occurs f 2 times, x 3 occurs f 3 times and so on. hence, the formula to calculate.
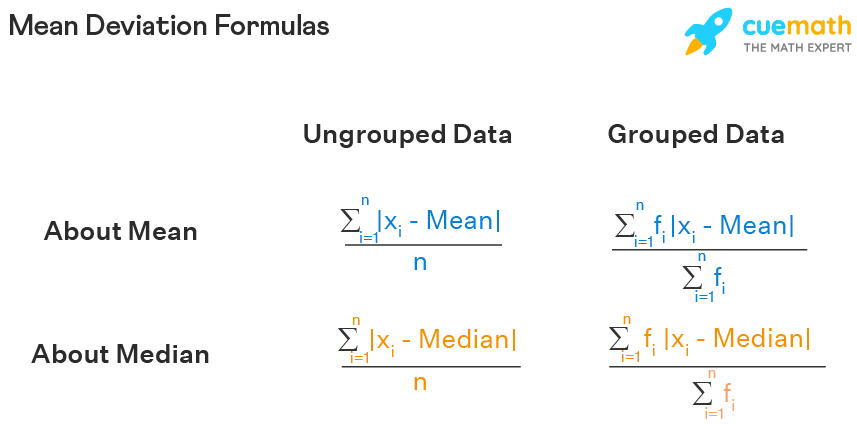
Mean Deviation Formula Definition Meaning Examples Step 1 – calculate the mean, median or mode value of the given data set. step 2 – then we must find the absolute difference between each value in the data set with the mean, ignoring the signs. step 3 – we then sum up all the deviations. step 4 – finally, we find the mean or average of those values found in step 3. Step deviation method; let us go through the formulas in these three methods given below: direct method. suppose x 1, x 2, x 3,…., x n be n observations with respective frequencies f 1, f 2, f 3,…., f n. this means, the observation x 1 occurs f 1 times, x 2 occurs f 2 times, x 3 occurs f 3 times and so on. hence, the formula to calculate. To calculate the mean deviation for grouped data and particularly for discrete distribution data, the following steps are followed: 1st step: the measure of central tendency about which mean deviation is to be calculated. let this measure be \ (a\). if this measure is mean, then it is calculated as,. Benefits of using mean deviation. the benefits of making use of mean deviation are: as it is based on all of the data values provided, it will provide a more accurate assessment of dispersion. it is simple to comprehend and compute. drawbacks of using mean deviation. as mean deviation cannot be further algebraically treated, it has lower.

Mean Deviation Formula To calculate the mean deviation for grouped data and particularly for discrete distribution data, the following steps are followed: 1st step: the measure of central tendency about which mean deviation is to be calculated. let this measure be \ (a\). if this measure is mean, then it is calculated as,. Benefits of using mean deviation. the benefits of making use of mean deviation are: as it is based on all of the data values provided, it will provide a more accurate assessment of dispersion. it is simple to comprehend and compute. drawbacks of using mean deviation. as mean deviation cannot be further algebraically treated, it has lower.

Comments are closed.