7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations

7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations Characteristics of sine and cosine functions. the sine and cosine functions have several distinct characteristics: they are periodic functions with a period of 2π. the domain of each function is (− ∞, ∞) and the range is [− 1, 1]. the graph of y = sin x is symmetric about the origin, because it is an odd function. The first is graphing the sine and cosine functions by hand and analyzing already graphed functions. students have to identify the amplitude, and period. the second sheet is the horizontal translations of graphing the sine and cosine functions. students have to identify the amplitude, period and phase shift.

7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations A vertical translation is of the form: y = sin(θ) a where a ≠ 0. or y = cos(θ) a. example: y = sin(θ) 5 is a sin graph that has been shifted up by 5 units. the graph y = cos(θ) − 1 is a graph of cos shifted down the y axis by 1 unit. a horizontal translation is of the form: y = sin(θ a) where a ≠ 0. The amplitude is maximum value minimum value 2 = 28. this graph also has a vertical and horizontal shift. in this section, we will explore both vertical and horizontal shifts. translating sine and cosine functions. just like other functions, sine and cosine curves can be translated to the left, right, up, and down. The standard trig equation for sine is y = a ⋅ sin[b(x − cπ)] d. in this, the variable a represents the amplitude. the variable b represents the period (2π b = period). now, the variable c represents what is known as the phase shift more commonly known as a horizontal translation. you shift the graph cπ units from the original parent. In the chapter on trigonometric functions, we examined trigonometric functions such as the sine function. in this section, we will interpret and create graphs of sine and cosine functions. graphing sine and cosine functions. recall that the sine and cosine functions relate real number values to the x and y coordinates of a point on the unit.
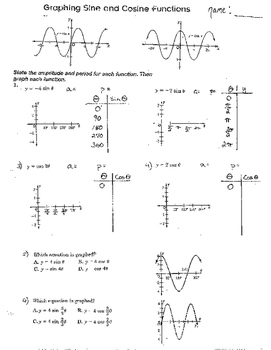
7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations The standard trig equation for sine is y = a ⋅ sin[b(x − cπ)] d. in this, the variable a represents the amplitude. the variable b represents the period (2π b = period). now, the variable c represents what is known as the phase shift more commonly known as a horizontal translation. you shift the graph cπ units from the original parent. In the chapter on trigonometric functions, we examined trigonometric functions such as the sine function. in this section, we will interpret and create graphs of sine and cosine functions. graphing sine and cosine functions. recall that the sine and cosine functions relate real number values to the x and y coordinates of a point on the unit. 10: graphs of trigonometric functions. key terms. basic graphs. amplitude: one half of the vertical distance between the maxima and minima of a sine or cosine graph. asymptote: any line that a function approaches closely without ever intersecting. fundamental period: the smallest interval over which a periodic function repeats itself. Figure 2.6.2.2. solution. the graph is the inverse of a basic sine function, which means a is a negative number. the amplitude of the graph is at y = − 5 and y = 5, or in other words, the minimum and maximum values on the graph are 5 away from the midline. therefore, the equation is y = − 5sin(x).

7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude 10: graphs of trigonometric functions. key terms. basic graphs. amplitude: one half of the vertical distance between the maxima and minima of a sine or cosine graph. asymptote: any line that a function approaches closely without ever intersecting. fundamental period: the smallest interval over which a periodic function repeats itself. Figure 2.6.2.2. solution. the graph is the inverse of a basic sine function, which means a is a negative number. the amplitude of the graph is at y = − 5 and y = 5, or in other words, the minimum and maximum values on the graph are 5 away from the midline. therefore, the equation is y = − 5sin(x).

Comments are closed.