7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations Some functions (like sine and cosine) repeat forever and are called periodic functions. the period goes from one peak to the next (or from any point to the next matching point): the amplitude is the height from the center line to the peak (or to the trough). or we can measure the height from highest to lowest points and divide that by 2. Answer. the value of b is 1, so the graph has a period of 2\pi, as does y = \sin x. the value of a is 1, so the graph has an amplitude of 1, as does y = \sin x. though the amplitude and the period are the same as the function y = \sin x, the graph is not exactly the same.
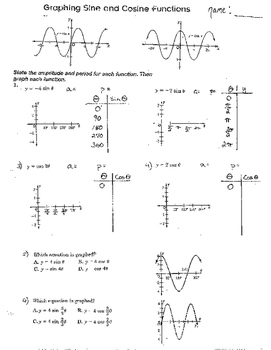
7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations In the standard graphs the difference between the maximum and minimum is \(1 ( 1)=2 ;\) one half of this is 1 so the amplitude of the standard sine and cosine functions is \(1 .\) the value of the amplitude is also the absolute value of the coefficient of the sine or cosine expression. in the standard graph, \(y=\sin x,\) the coefficient of the. In the chapter on trigonometric functions, we examined trigonometric functions such as the sine function. in this section, we will interpret and create graphs of sine and cosine functions. graphing sine and cosine functions. recall that the sine and cosine functions relate real number values to the x and y coordinates of a point on the unit. As we have seen, trigonometric functions follow an alternating pattern between hills and valleys. the amplitude of a trigonometric function is half the distance from the highest point of the curve to the bottom point of the curve: \[ \text{(amplitude)} = \frac{ \text{(maximum) (minimum)} }{2}.\] for example, if we consider the graph of \(y. Graphing sine and cosine functions. recall that the sine and cosine functions relate real number values to the \(x\) and \(y\) coordinates of a point on the unit circle. so what do they look like on a graph on a coordinate plane? let’s start with the sine function. we can create a table of values and use them to sketch a graph.
7 Graphing Trigonometric Trig Sine Cosine Functions Amplitude Translations As we have seen, trigonometric functions follow an alternating pattern between hills and valleys. the amplitude of a trigonometric function is half the distance from the highest point of the curve to the bottom point of the curve: \[ \text{(amplitude)} = \frac{ \text{(maximum) (minimum)} }{2}.\] for example, if we consider the graph of \(y. Graphing sine and cosine functions. recall that the sine and cosine functions relate real number values to the \(x\) and \(y\) coordinates of a point on the unit circle. so what do they look like on a graph on a coordinate plane? let’s start with the sine function. we can create a table of values and use them to sketch a graph. 10: graphs of trigonometric functions. key terms. basic graphs. amplitude: one half of the vertical distance between the maxima and minima of a sine or cosine graph. asymptote: any line that a function approaches closely without ever intersecting. fundamental period: the smallest interval over which a periodic function repeats itself. Match each function in column i with the appropriate description in column ii. i. y = 4 sin(3x 2) ii. a. amplitude = 2, period = π 2, phase shift = ¾.
Comments are closed.