62v35v5 4 12 Two Circles Touch Each Other Externally Of Radii 8 Cm And 5 Cm Respectively

Two Circles Of Radius 5 And 8cm Touch Each Other Externally Mathskey The radii of both circles are 12 cm and 8 cm. both circles touch each other at point a externally. mn is the common tangent of both circles. calculations: according to the question, let the centers of circles be p and q respectively. join p to q and m. join q to n. draw pt ⊥ qn. now pt = mn, as they are opposite sides of the rectangle ptnm. When two circles touch each other externally then the distance between their centres is given by the sum of their radii . distance between centres = radius of 1 st circle radius of 2 nd circle . calculation: let ‘r’ be the radius of 2 nd circle. according to the question, ⇒ 8 = 3 r. ⇒ r = 8 – 3 = 5 cm. ∴ the radius of other.

If Two Circles Touch Each Other Externally Or Internally Then The Two If two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres. two circles having radii 3.5 cm and 4.8 cm touch each other internally. find the distance between their centres. in the given figure, the circles with centres p and q touch each other at r. Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. Am = ap – pm = ap – bq = 8 cm – 5 cm = 3 cm. since the two circles touch each other externally, the distance between their centers is equal to sum of their radii. ab = 8 cm 5 cm = 13 cm. applying pythagoras theorem in right Δmab, we have: pq = bm = 12.64. hence, the length of the common tangent is 12.64 cm. If two circles with radii 8 cm and 3 cm, respectively, touch internally, then find the distance between their centers. if two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres. two circles having radii 3.5 cm and 4.8 cm touch each other internally. find the distance between their centres.

Two Circles Of Radii 5 Cm And 2 8 Cm Touch Each Other Find The Am = ap – pm = ap – bq = 8 cm – 5 cm = 3 cm. since the two circles touch each other externally, the distance between their centers is equal to sum of their radii. ab = 8 cm 5 cm = 13 cm. applying pythagoras theorem in right Δmab, we have: pq = bm = 12.64. hence, the length of the common tangent is 12.64 cm. If two circles with radii 8 cm and 3 cm, respectively, touch internally, then find the distance between their centers. if two circles with radii 8 cm and 3 cm respectively touch externally, then find the distance between their centres. two circles having radii 3.5 cm and 4.8 cm touch each other internally. find the distance between their centres. Now adding the radius of both the given circles, we have. r1 r2 = 3 2 = 5 r 1 r 2 = 3 2 = 5. this shows that the distance between the centers of the given circles is equal to the sum of their radii. this is only possible if the circles touche each other externally, as shown in the figure. two circles touching internally equation of a. Given: two circles touch each other externally. radius of first circle with centre a = 18 cm. radius of second circle with centre b = 8 cm. formula used: length of direct common tangent = d 2 − (r 1 − r 2) 2. where, d = r 1 r 2 , r 1 = radius of first circle ,r 2 = radius of second circle. calculation:.

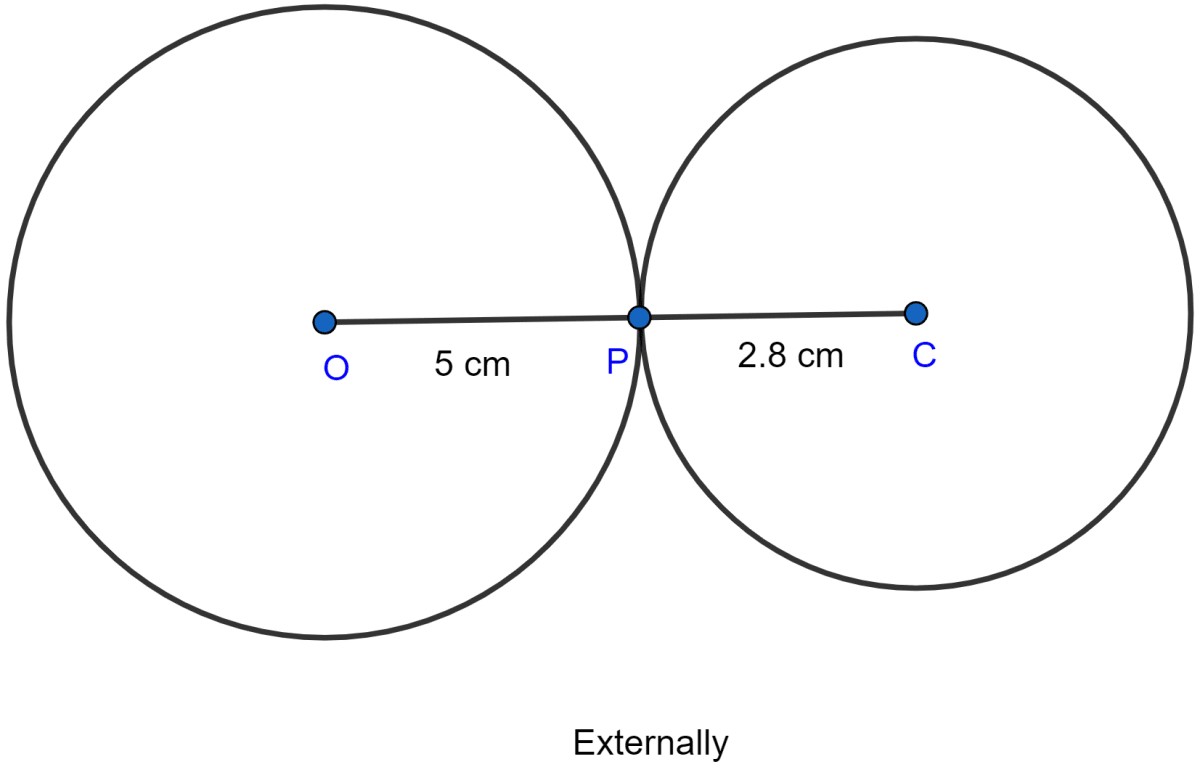
Two Circles Of Radii 5 Cm And 2 8 Cm Touch Each Other Find Knowledgeboat Now adding the radius of both the given circles, we have. r1 r2 = 3 2 = 5 r 1 r 2 = 3 2 = 5. this shows that the distance between the centers of the given circles is equal to the sum of their radii. this is only possible if the circles touche each other externally, as shown in the figure. two circles touching internally equation of a. Given: two circles touch each other externally. radius of first circle with centre a = 18 cm. radius of second circle with centre b = 8 cm. formula used: length of direct common tangent = d 2 − (r 1 − r 2) 2. where, d = r 1 r 2 , r 1 = radius of first circle ,r 2 = radius of second circle. calculation:.