3con14 Matematicas E Valor Absoluto Formulas

3con14 Matemáticas E Valor Absoluto Fórmulas E · valor absoluto [fórmulas] valor absoluto (pdf) este obra está bajo una licencia de creative commons reconocimiento nocomercial 4.0 internacional. de que sirve acumular conocimiento si no se comparte. " todo lo que no se da se pierde " (proverbio indio) (cc) 1998 2018, 3con14 | jesús plaza m. 3con14 matemáticas de. E · elementos esféricos [fórmulas] e · Álgebra i [fórmulas] e · geometría i [fórmulas] e · gráficas i [fórmulas] e · valor absoluto [fórmulas] e · gráficas i transformaciones [fórmulas] e · ternas pitagóricas [fórmulas] b · hoja 006 ejercicios resueltos de ecuaciones exponenciales.

3con14 Matemáticas A Intervalos Semirrectas Valor Absoluto Guía Valor absoluto. el valor absoluto de un número a , escrito |a|, es la distancia de a al cero en la recta real. una distiancia es siempre positiva o cero, de modo que tenemos |a| ≥ 0 para todo número real a. de modo que tenemos esta definición: |a| = { a si a ≥ 0 a si a < 0. Ejemplo 2: ecuaciones con más de un valor absoluto. veamos una ecuación con valor absoluto que tiene múltiples términos: |2x 1| = 7. igual que antes, consideramos cada caso: case 1: 2x 1 = 7 → 2x = 6 → x = 3. case 2: 2x 1 = 7 → 2x = 8 → x = 4. las soluciones para esta ecuación valor absoluto son x = 3 y x = 4. A continuación las principales propiedades del valor absoluto: 1) el valor absoluto de un número siempre es positivo o 0, por lo tanto: │x│≥ 0. 2) el valor absoluto de cero también es cero, es decir │0│ = 0, por lo tanto se puede afirmar que: │x│ = 0, si y solo si x = 0. 3) para todo número x que pertenece al conjunto de los. 2. función valor absoluto. la función valor absoluto es la función \(f:\mathbb{r}\to [0, \infty)\) dada por. también, podemos definir la función por partes: la gráfica de la función es. esta función es continua en todos los reales y derivable en todos los reales excepto en \(x=0\). 3. algunas propiedades. veamos algunas de las.
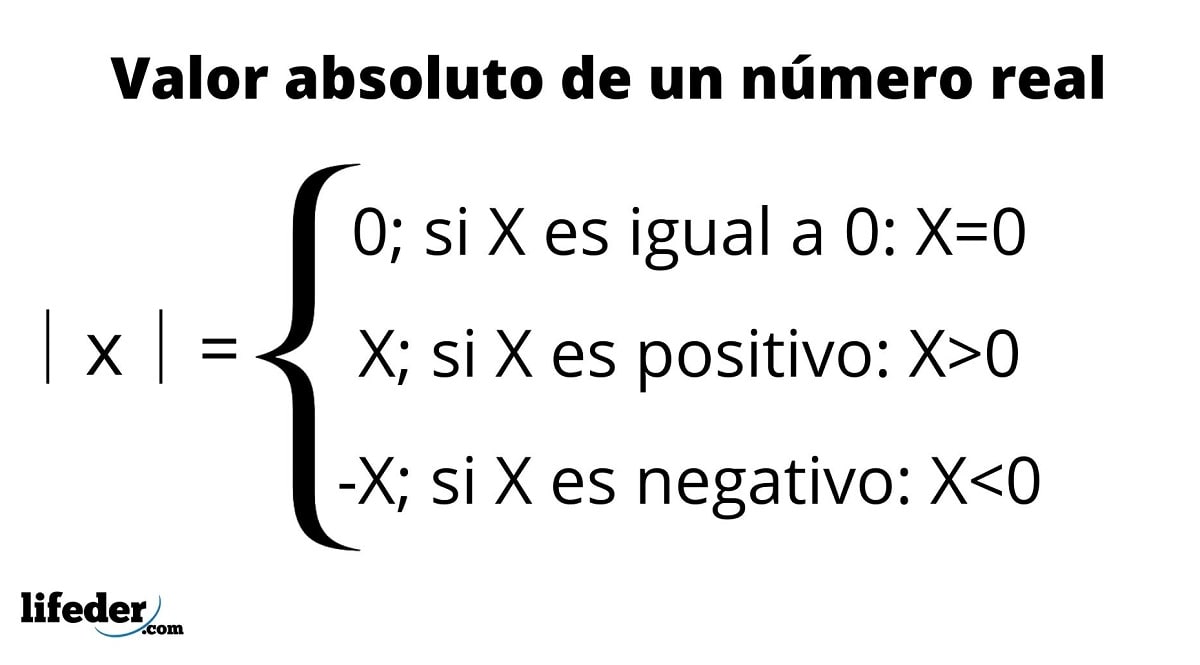
Valor Absoluto Propiedades Ejemplos Ejercicios A continuación las principales propiedades del valor absoluto: 1) el valor absoluto de un número siempre es positivo o 0, por lo tanto: │x│≥ 0. 2) el valor absoluto de cero también es cero, es decir │0│ = 0, por lo tanto se puede afirmar que: │x│ = 0, si y solo si x = 0. 3) para todo número x que pertenece al conjunto de los. 2. función valor absoluto. la función valor absoluto es la función \(f:\mathbb{r}\to [0, \infty)\) dada por. también, podemos definir la función por partes: la gráfica de la función es. esta función es continua en todos los reales y derivable en todos los reales excepto en \(x=0\). 3. algunas propiedades. veamos algunas de las. El valor absoluto o magnitud de x ∈ r, denotado por |x| es un número no negativo definido por la siguiente regla: ejemplos: en realidad ∀ x ∈ r, x ≠ 0, el valor absoluto |x| es la distancia en la recta numérica entre “0” y “x”. ejemplo: definir |x−a|; a ∈ r. para la resolución de problemas se debe tener en cuenta lo. 3con14 matemáticas de secundaria y bachillerato. resúmenes, construcciones geogebra. e · valor absoluto [fórmulas] publicado en fórmulas. valor absoluto.

Valor Absoluto Ejercicios Resueltos Para Principiantes Youtube El valor absoluto o magnitud de x ∈ r, denotado por |x| es un número no negativo definido por la siguiente regla: ejemplos: en realidad ∀ x ∈ r, x ≠ 0, el valor absoluto |x| es la distancia en la recta numérica entre “0” y “x”. ejemplo: definir |x−a|; a ∈ r. para la resolución de problemas se debe tener en cuenta lo. 3con14 matemáticas de secundaria y bachillerato. resúmenes, construcciones geogebra. e · valor absoluto [fórmulas] publicado en fórmulas. valor absoluto.

Comments are closed.