2 Maximum Likelihood For Regression Coefficients Part 1 Of 3

2 Maximum Likelihood For Regression Coefficients Part 1 Of 3 Youtube About press copyright contact us creators advertise developers terms privacy policy & safety how works test new features nfl sunday ticket press copyright. 3. ˘n(0;˙2), and is independent of x. 4. is independent across observations. a consequence of these assumptions is that the response variable y is indepen dent across observations, conditional on the predictor x, i.e., y 1 and y 2 are independent given x 1 and x 2 (exercise 1).

Self Study Maximum Likelihood Estimation Of Coefficients For Linear Maximum likelihood estimator(s) 1. 0 b 0 same as in least squares case 2. 1 b 1 same as in least squares case 3. ˙ 2 ˙^2 = p i (y i y^ i)2 n 4.note that ml estimator is biased as s2 is unbiased and s2 = mse = n n 2 ^˙2. The first entries of the score vector are the th entry of the score vector is the hessian, that is, the matrix of second derivatives, can be written as a block matrix let us compute the blocks: and finally, therefore, the hessian is by the information equality, we have that but and, by the law of iterated expectations, thus, as a consequence, the asymptotic covariance matrix is. N 1. nll(y j x; w; b) = x jyibi=1wtxij n log(2b)thus, the maximum likelihood estimate in this case can be obtained by minimising the sum of the absolute values of the residuals, which is the same objective we discussed in the last lecture in the context f. Maximum likelihood estimation. the likelihood function can be maximized w.r.t. the parameter(s) Θ, doing this one can arrive at estimators for parameters as well. l({xi }n i=1 , Θ) =. i=1 n f (xi ; Θ) • to do this, find solutions to (analytically or by following gradient) dl({x i }n ,Θ) i=1 = 0. dΘ.

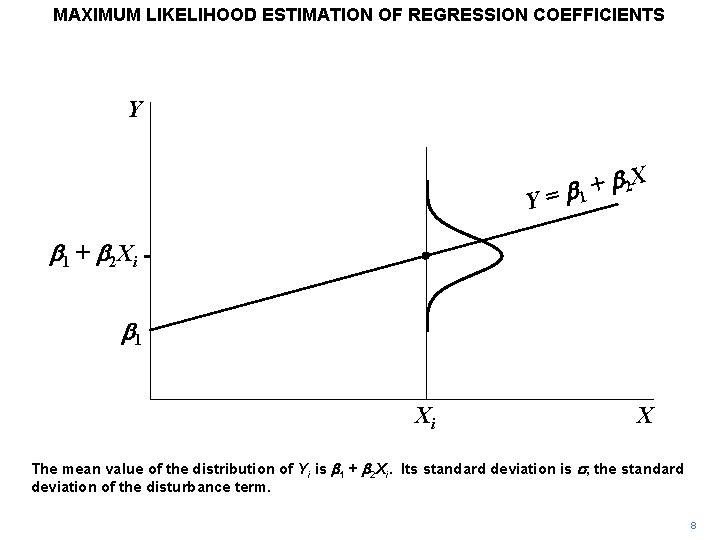
Maximum Likelihood Estimation Of Regression Coefficients Y Y N 1. nll(y j x; w; b) = x jyibi=1wtxij n log(2b)thus, the maximum likelihood estimate in this case can be obtained by minimising the sum of the absolute values of the residuals, which is the same objective we discussed in the last lecture in the context f. Maximum likelihood estimation. the likelihood function can be maximized w.r.t. the parameter(s) Θ, doing this one can arrive at estimators for parameters as well. l({xi }n i=1 , Θ) =. i=1 n f (xi ; Θ) • to do this, find solutions to (analytically or by following gradient) dl({x i }n ,Θ) i=1 = 0. dΘ. Properties of mle. maximum likelihood estimator : = arg max. best explains data we have seen. does not attempt to generalize to data not yet observed. often used when sample size is large relative to parameter space. potentially biased (though asymptotically less so, as → ∞) consistent: lim 9 − < = 1 where > 0. f. I))2: thus, the principle of maximum likelihood is equivalent to the least squares criterion for ordinary linear regression. the maximum likelihood estimators and give the regression line y^ i= ^ x^ i: exercise 7. show that the maximum likelihood estimator for ˙2 is ^˙2 mle = 1 n xn k=1 (y i y^ )2: 186.