2 8 1 Quicksort Algorithm

Quicksort Understanding The Quicksort Algorithm And Implementation The time complexity of quick sort is o(n log n) on average case, but can become o(n^2) in the worst case. the space complexity of quick sort in the best case is o(log n), while in the worst case scenario, it becomes o(n) due to unbalanced partitioning causing a skewed recursion tree that requires a call stack of size o(n). variationtime complexitys. Kotlin. 1. introduction. in this tutorial, we’re going to look at the quicksort algorithm and understand how it works. quicksort is a divide and conquer algorithm. this means that each iteration works by dividing the input into two parts and then sorting those, before combining them back together.
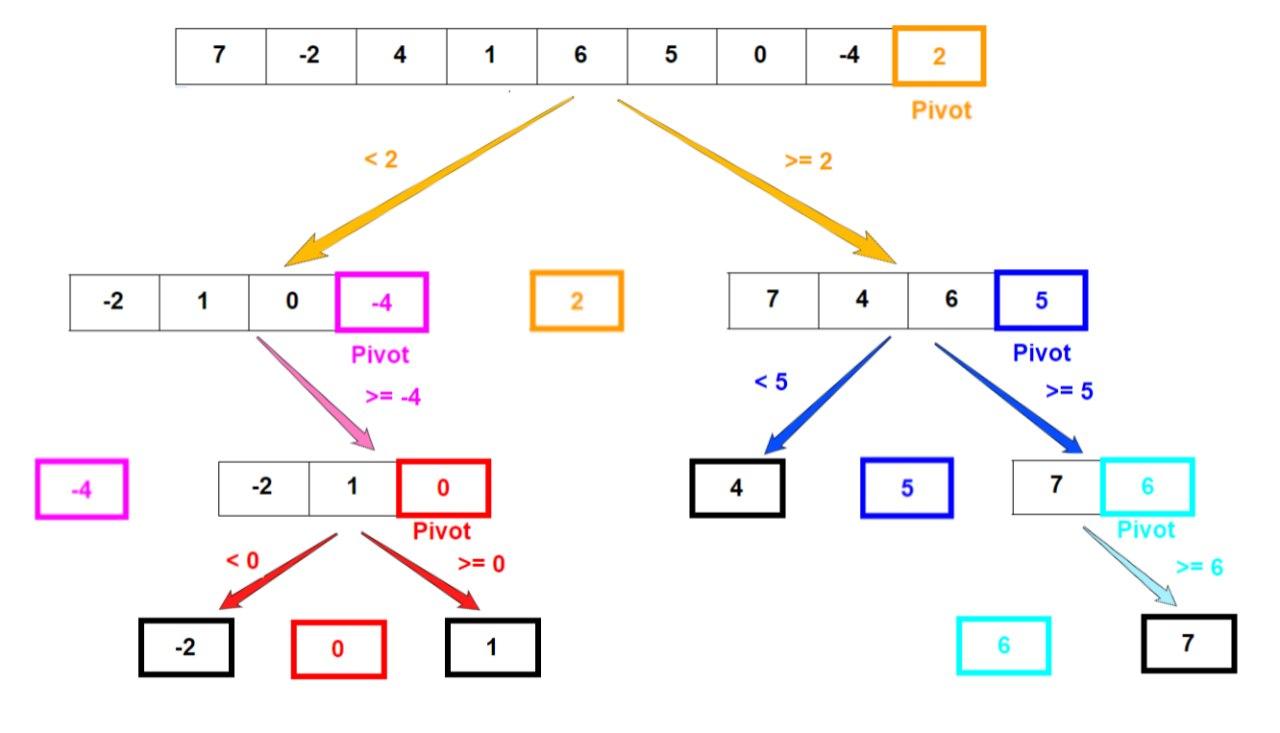
Quicksort In Javascript Quicksort code in python, java, and c c . pivot = array[high] # pointer for greater element. i = low 1 # traverse through all elements # compare each element with pivot for j in range(low, high): if array[j] <= pivot: # if element smaller than pivot is found # swap it with the greater element pointed by i. Algorithm : quicksort. 1. pick the last element from the array. this is termed as the pivot. 2. place pivot it in its final position in the array, such that. the elements to its left are less than itself and the elements to the right of the pivot is greater than itself. 3. partition the array at the pivot. In the following example, the elements [3, 7, 1, 8, 2, 5, 9, 4, 6] are sorted this way. you will see how the optimized quicksort algorithm performs with other. Khan academy.
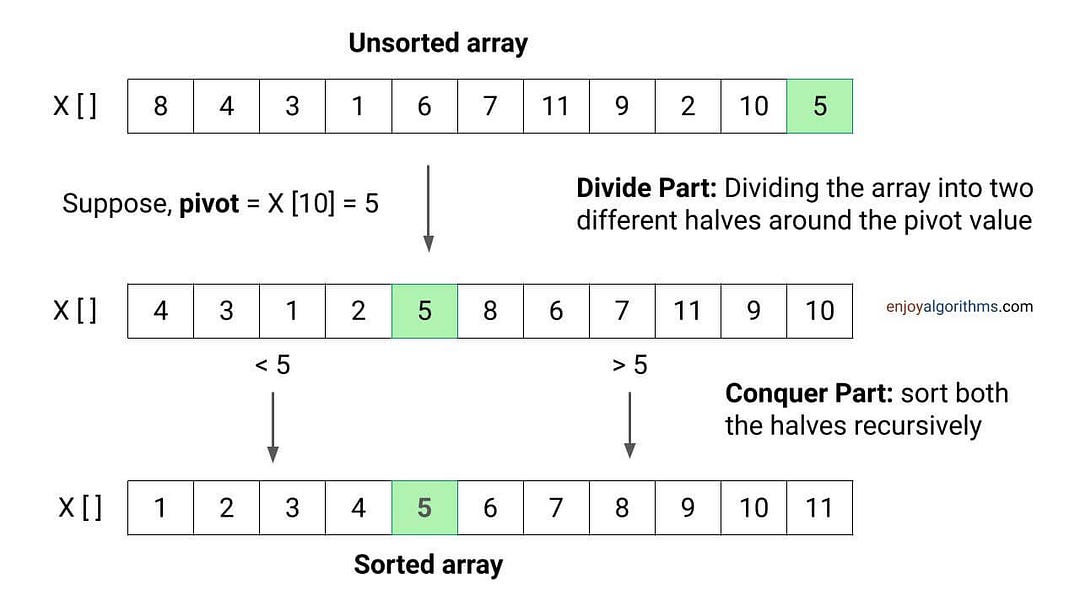
Quick Sort Algorithm In the following example, the elements [3, 7, 1, 8, 2, 5, 9, 4, 6] are sorted this way. you will see how the optimized quicksort algorithm performs with other. Khan academy. The best case time complexity of quicksort is o(n.log(n)). the best case happens when the pivot divides the array into two nearly equal pieces. now each recursive call processes a list of half the size. t(n) = 2 t(n 2) cn = o(n.log(n)) the auxiliary space required by the quicksort algorithm is o(n) for the call stack. must read:. Quick sort algorithm is often the best choice for sorting because it works efficiently on average o(nlogn) time complexity. it is also one of the best algorithms to learn divide and conquer approach. in this blog, you will learn: 1) how quick sort works? 2) how to choose a good pivot? 3) best, worst, and average case analysis 4) space complexity and properties of quicksort.

Comments are closed.