2 2 Derivative Graphically And Numerically Understanding The

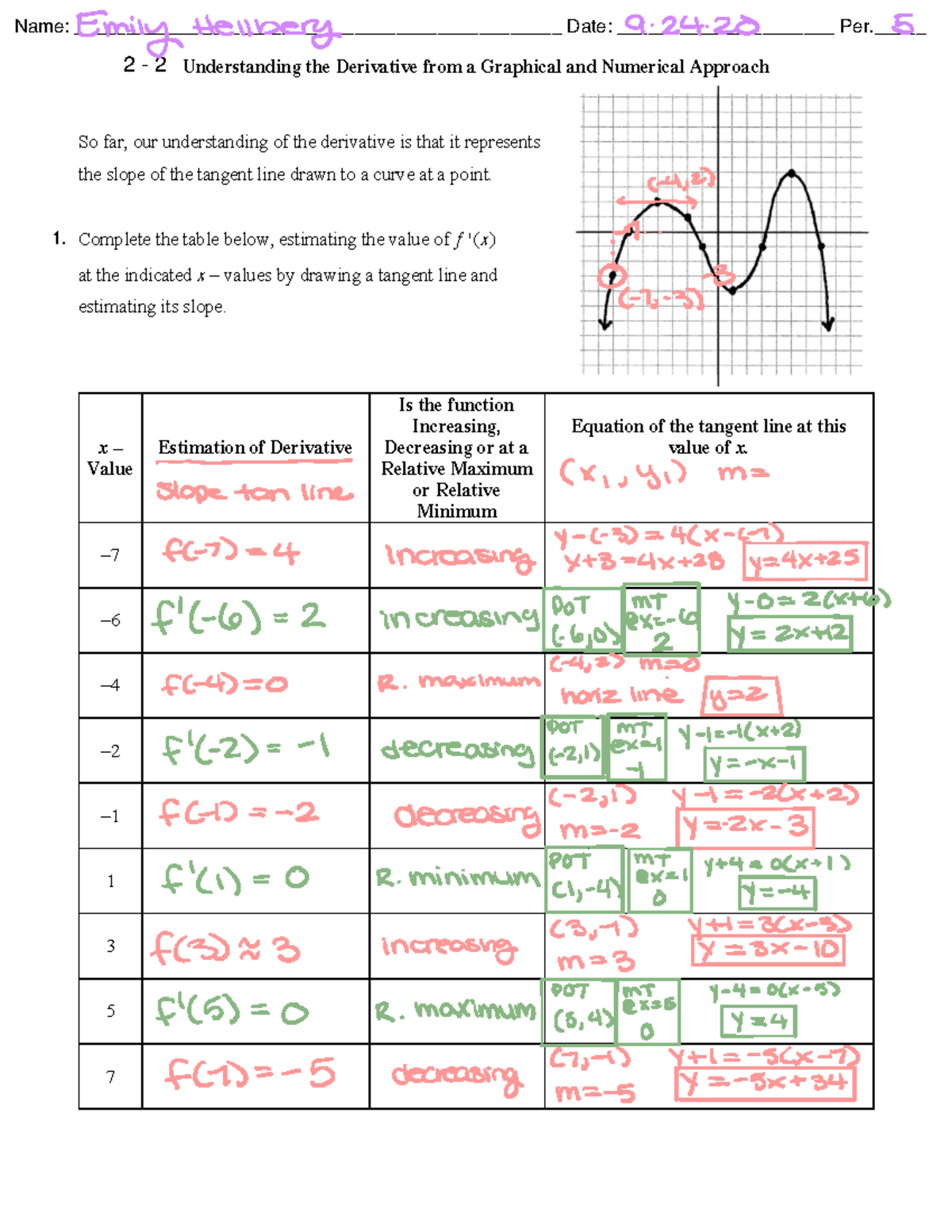
2 2 Derivative Graphically And Numerically Understanding The Label a point, a, on the graph of y = f(x) where the derivative is negative. label a point, b, on the graph of y = f(x) where the value of the function is negative. label a point, c, on the graph of y = f(x) where the derivative is greatest in value. label a point, d, on the graph of y = f(x) where the derivative is zero. Example 44: understanding the graph of the derivative. consider the graph of f(x) and its derivative, f′(x), in figure 2.12 (a). use these graphs to find the slopes of the tangent lines to the graph of f at x = 1, x = 2, and x = 3. figure 2.12: graphs of f and f′ in example 44, along with tangent lines in (b). solution.

Derivatives Numerically And Graphically Youtube Determining the graph of a derivative of a function. suppose a function is f (x)=x^3 12x 3 f (x) = x3 −12x 3 and its graph is as follows: forget the equation for a moment and just look at the graph. now, to find the graph of {f}' f ′ from the above graph, we have to find two kinds of very important points. The derivative of a function describes the function's instantaneous rate of change at a certain point. another common interpretation is that the derivative gives us the slope of the line tangent to the function's graph at that point. learn how we define the derivative using limits. learn about a bunch of very useful rules (like the power, product, and quotient rules) that help us find. Single point by graphical and numerical methods • write equations of tangent lines and normal lines 2: 2.2 tangent lines and the derivative • use limit definition of the derivative, proper notation to find the general form of a derivative • analyze function behavior using the derivative. 3. 2.3 understanding the derivative and linear. Reading the derivative’s graph. posted on october 26, 2012 by lin mcmullin. a very typical calculus problem is given the equation of a function, to find information about it (extreme values, concavity, increasing, decreasing, etc., etc.). this is usually done by computing and analyzing the first derivative and the second derivative.

Calculus Df1 Derivatives Graphically And Numerically Youtube Single point by graphical and numerical methods • write equations of tangent lines and normal lines 2: 2.2 tangent lines and the derivative • use limit definition of the derivative, proper notation to find the general form of a derivative • analyze function behavior using the derivative. 3. 2.3 understanding the derivative and linear. Reading the derivative’s graph. posted on october 26, 2012 by lin mcmullin. a very typical calculus problem is given the equation of a function, to find information about it (extreme values, concavity, increasing, decreasing, etc., etc.). this is usually done by computing and analyzing the first derivative and the second derivative. Definition. let f f be a function. the derivative function, denoted by {f}^ {\prime }, f ′, is the function whose domain consists of those values of x x such that the following limit exists: {f}^ {\prime }\left (x\right)=\underset {h\to 0} {\text {lim}}\frac {f\left (x h\right) f\left (x\right)} {h}. f ′(x) = h→0lim hf (x h)−f (x). a. 2.2. interpretations of the derivative. the previous section defined the derivative of a function and gave examples of how to compute it using its definition (i.e., using limits). the section also started with a brief motivation for this definition, that is, finding the instantaneous velocity of a falling object given its position function.

2 2 Finding Limits Graphically And Numerically Youtube Definition. let f f be a function. the derivative function, denoted by {f}^ {\prime }, f ′, is the function whose domain consists of those values of x x such that the following limit exists: {f}^ {\prime }\left (x\right)=\underset {h\to 0} {\text {lim}}\frac {f\left (x h\right) f\left (x\right)} {h}. f ′(x) = h→0lim hf (x h)−f (x). a. 2.2. interpretations of the derivative. the previous section defined the derivative of a function and gave examples of how to compute it using its definition (i.e., using limits). the section also started with a brief motivation for this definition, that is, finding the instantaneous velocity of a falling object given its position function.