11 Two Circles Touch Each Other Internally Prove That The Tangents

11 Two Circles Touch Each Other Internally Prove That The Tangents To prove that the lengths of tangents drawn from any point on the common tangent to two internally touching circles are equal, we can follow these structured steps: 1 let the two circles be denoted as circle 1 with center c 1 c {1} c 1 and circle 2 with center c 2 c {2} c 2 . Two circles touch each other externally at point p. q is a point on the common tangent through p. prove that the tangents qa and qb are equal. q. what is the maximum number of common tangents that can be drawn to two circles of different radii, touching each other internally?.

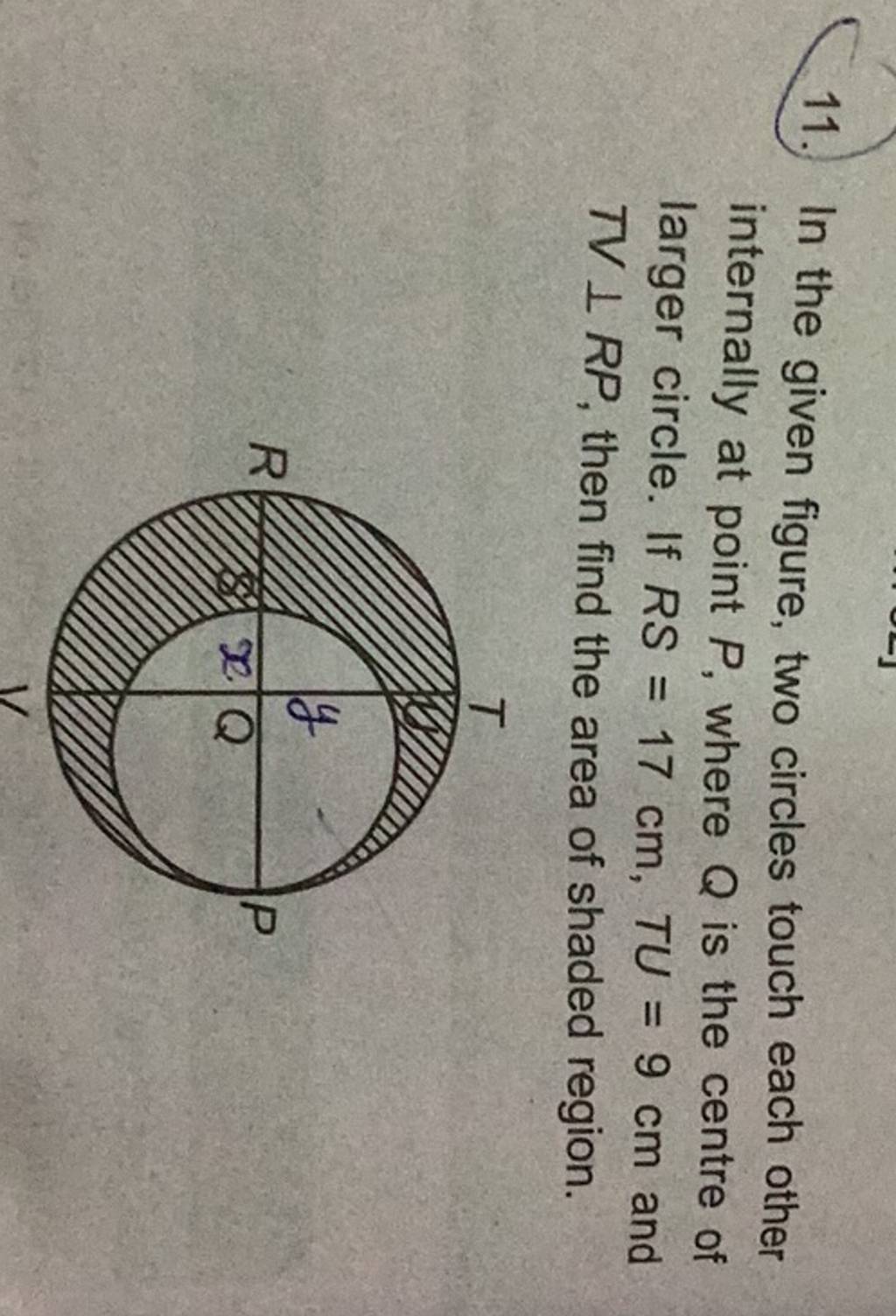
11 In The Given Figure Two Circles Touch Each Other Internally At Point Two circles are said to touch each other if they have only one point common – a common tangent can then be drawn to both the circles at that point. consider the following figure, where two circles s 1 and s 2 (with radii r 1 and r 2) touch each other externally at p. in this case, the distance between o 1 and o 2 (their centers) is r 1 r 2. Two circle with centres o and o' are drawn to intersect each other at points a and b. centre o of one circle lies on the circumference of the other circle and cd is drawn tangent to the circle with centre o' at a. prove that oa bisects angle bac. two circles touch each other internally at a point p. 3. if two circles touch each other internally. number of direct common tangents = 1. number of transverse common tangents = 0. 4. if two circles intersect each other at two points. number of direct common tangents = 2. number of transverse common tangents = 0. 5. if one circle lies completely inside the other circle. number of direct common. If two given circles are touching each other internally, use this example to understand the concept of internally toucheing circles. consider the given circles. x2 y2 2x– 8 = 0 – – – (i) x 2 y 2 2 x – 8 = 0 – – – (i) and x2 y2– 6x 6y– 46 = 0 – – – (ii) x 2 y 2 – 6 x 6 y – 46 = 0 – – – (ii) let.

If Two Circles Touch Each Other Externally Or Internally Then The Two 3. if two circles touch each other internally. number of direct common tangents = 1. number of transverse common tangents = 0. 4. if two circles intersect each other at two points. number of direct common tangents = 2. number of transverse common tangents = 0. 5. if one circle lies completely inside the other circle. number of direct common. If two given circles are touching each other internally, use this example to understand the concept of internally toucheing circles. consider the given circles. x2 y2 2x– 8 = 0 – – – (i) x 2 y 2 2 x – 8 = 0 – – – (i) and x2 y2– 6x 6y– 46 = 0 – – – (ii) x 2 y 2 – 6 x 6 y – 46 = 0 – – – (ii) let. Note: let two circles with centres o and p touch each other at t. let ot = r1 and pt = r2 and r1 > r2. let the distance between their centres = op = d. it is clear from the figures that. • when the circles touch externally, d = r 1 r 2. • when the circles touch internally, d = r 1 r 2. 10th grade math. You may be asked to show that two circles are touching, and say whether they're touching internally or externally. to do this, you need to work out the radius and the centre of each circle. if the.