1 7 Solving Absolute Value Equations Ms Zeilstra S Math Classes Algebra 1. geometry. algebra 2. honors algebra 2. forums. psat prep. welcome! on this website, you will find notes, worksheets, and activities for ms. zeilstra's math classes. use the navigation tabs above to find exactly what you're looking for!. We can verify that our four answers or solutions are = 4 x = – \,4, 2, and , by graphing the two functions and looking at their points of intersections. absolute value equations practice problems with answers. solve absolute value equations quickly and easily with these simple tips and tricks. learn how to separate & components and.
1 7 Solving Absolute Value Equations Ms Zeilstra S Math Classes The absolute value of a number is its distance from zero on the number line. the absolute value of a number n is written as | n | and | n | ≥ 0 for all numbers. absolute values are always greater than or equal to zero. we learned that both a number and its opposite are the same distance from zero on the number line. The next step is to ditch the absolute value bars and solve the following equations: positive: 2x 4=2 and negative: 2x 4= 2. now you have two solutions: x=3 and x=1. step three: check your answer. the final step is to plug both solutions, x=3 and x=1, into the original equation |2x 4| 8=10 and verify that each solution checks out and you are. For problems 1 – 5 solve each of the equation. for problems 6 & 7 find all the real valued solutions to the equation. here is a set of practice problems to accompany the absolute value equations section of the solving equations and inequalities chapter of the notes for paul dawkins algebra course at lamar university. 1. isolate the absolute value expression to one side of the equal sign. 2. set the inside of the absolute value equal to and to the value on the other side of the equal sign (remove the absolute value bars in this step). 3. if needed, solve for the variable in these 2 new equations. 4.
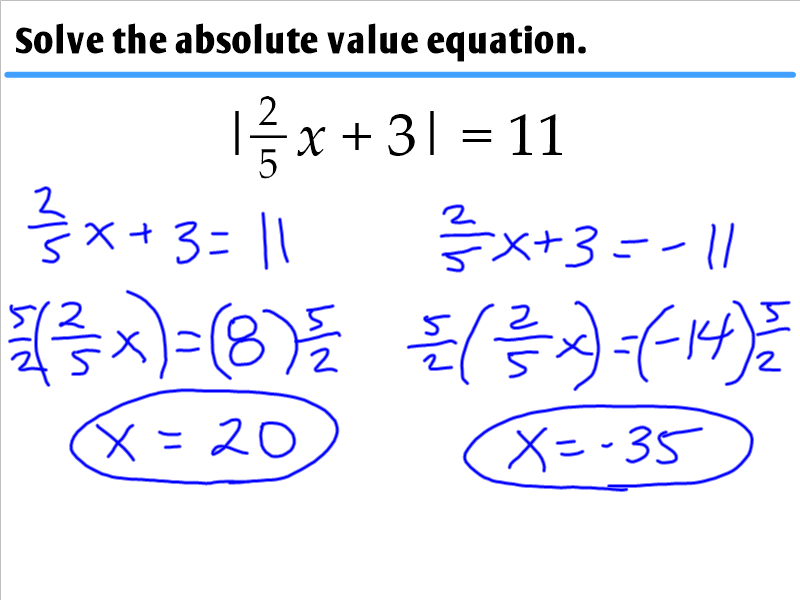
1 7 Solving Absolute Value Equations Ms Zeilstra S Math Classes For problems 1 – 5 solve each of the equation. for problems 6 & 7 find all the real valued solutions to the equation. here is a set of practice problems to accompany the absolute value equations section of the solving equations and inequalities chapter of the notes for paul dawkins algebra course at lamar university. 1. isolate the absolute value expression to one side of the equal sign. 2. set the inside of the absolute value equal to and to the value on the other side of the equal sign (remove the absolute value bars in this step). 3. if needed, solve for the variable in these 2 new equations. 4. Using the distance definition to solve an absolute value equation. solve |p 4|=5. the expression |p 4| represents the distance between p and 4. the equation |p 4|=5 can be solved by finding all real numbers that are 5 units from 4. as shown in figure 2.16, these numbers are − 1 and 9. the solution set is {− 1,9}. An absolute value equation is an equation that contains an absolute value expression. the equation $$\left | x \right |=a$$ has two solutions x = a and x = a because both numbers are at the distance a from 0. to solve an absolute value equation as $$\left | x 7 \right |=14$$ you begin by making it into two separate equations and then solving.
Comments are closed.