рџљёecuaciones De Primer Grado 01 Con Una Incгіgnita Parte Uno вљ пёџвўmuy

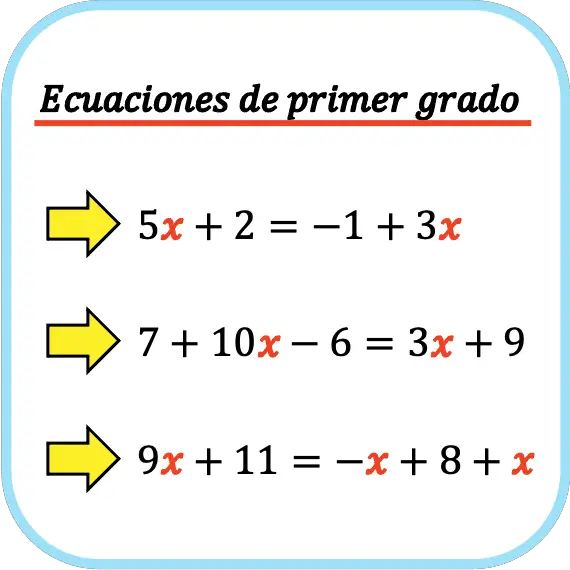
Ecuaciones De Primer Grado Ecuaciones de primer grado ejerciciosecuaciones de primer grado ejercicios resueltosecuaciones de primer grado con una incógnitacuáles son las ecuaciones de. Aprenderemos a resolver ecuaciones de primer grado con una incógnita: sencillas, con paréntesis, con denominadores y con ambos a la vez. introducción: concepto de ecuaciónecuaciones equivalentesregla de la suma y regla del productoecuaciones de primer grado sin paréntesis ni denominadores¿qué ocurre si al resolver una ecuación obtenemos 0=0?¿qué ocurre si al resolver una ecuación.

D0 B2 D1 81 D0 B5 D0 Bc D0 B8 D1 80 D0 Bd D1 8b D0 B9 D0 B4 D0 B5 D0 Una ecuación de primer grado es una igualdad matemática con una o más incógnitas. dichas incógnitas deben ser despejadas o resueltas para encontrar el valor numérico de la igualdad. las ecuaciones de primer grado reciben este nombre porque sus variables (incógnitas) están elevadas a la primera potencia (x1), que suele representarse solo. Resolver esta ecuación de primer grado con una incógnita: solución: se reducen todos los términos a común denominador. el mínimo común múltiplo de 3, 2 y 5 es 30: multiplicando todos los términos por 30, se eliminan los denominadores y la igualdad se mantiene: se eliminan los paréntesis, multiplicando los factores de cada uno por sus. Las ecuaciones de primer grado con una incógnita, son parte fundamental del álgebra. ellas aparecerán de diferentes maneras, dentro de una amplia variedad de temas. por lo tanto, es más que importante comprender ya desde el comienzo, las reglas que se aplican para resolver este tipo de ecuaciones. El doble de x es 2x, luego obtenemos la ecuación. 2x 5 = 35. resolvemos la ecuación: 2x = 35 − 5 2x = 30 x = 30 2 = 15. por tanto el número es el 15. sea x el número buscado, su consecutivo (el siguiente) se obtiene al sumarle 1. como la suma de x y de su consecutivo debe ser 51, tenemos: x (x 1) = 51.

Ecuaciones De Primer Grado Ejercicios Resueltos Como 55 Off Las ecuaciones de primer grado con una incógnita, son parte fundamental del álgebra. ellas aparecerán de diferentes maneras, dentro de una amplia variedad de temas. por lo tanto, es más que importante comprender ya desde el comienzo, las reglas que se aplican para resolver este tipo de ecuaciones. El doble de x es 2x, luego obtenemos la ecuación. 2x 5 = 35. resolvemos la ecuación: 2x = 35 − 5 2x = 30 x = 30 2 = 15. por tanto el número es el 15. sea x el número buscado, su consecutivo (el siguiente) se obtiene al sumarle 1. como la suma de x y de su consecutivo debe ser 51, tenemos: x (x 1) = 51. A continuación se resuelven ecuaciones de primer grado cuya dificultad va aumentado: ecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). en la parte i, las ecuaciones son más cortas y se explican todos los pasos. pretenden estar ordenadas de menor. Hola, en esta clase revolveremos una ecuación de primer grado con una incógnita de 2 formas diferentes, la forma "larga" y la "corta" de ustedes dependerá cu.

рџљёecuaciones De Primer Grado 01 Con Una Incгіgnita Parte Uno вљ пёџвўmuy A continuación se resuelven ecuaciones de primer grado cuya dificultad va aumentado: ecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados (unos dentro de otros). en la parte i, las ecuaciones son más cortas y se explican todos los pasos. pretenden estar ordenadas de menor. Hola, en esta clase revolveremos una ecuación de primer grado con una incógnita de 2 formas diferentes, la forma "larga" y la "corta" de ustedes dependerá cu.

Resueltos Ejemplos De Ecuaciones De Primer Grado Con Una Incognita

Ecuaciones De Primer Grado Ecuaciones De Primer Grado